ML101.02: Linear Regression

Trở lại với ví dụ về bài toán dự đoán giá căn hộ ở bài trước. Ta có bảng dữ liệu như sau:
| Diện tích (m2) | Số phòng | Giá (tỉ đồng) |
|---|---|---|
| 60 | 2 | 1,8 |
| 70 | 3 | 2,4 |
| 50 | 1 | 1,2 |
| 65 | 3 | 2,2 |
Để dễ tưởng tượng, đầu tiên ta xét bài toán chỉ với một biến đầu vào và một biến đầu ra đó là diện tích và giá:
| Diện tích (m2) | Giá (tỉ đồng) |
|---|---|
| 60 | 1,8 |
| 70 | 2,4 |
| 50 | 1,2 |
| 65 | 2,2 |
Vẽ các điểm trên hệ tọa độ hai chiều ta được:
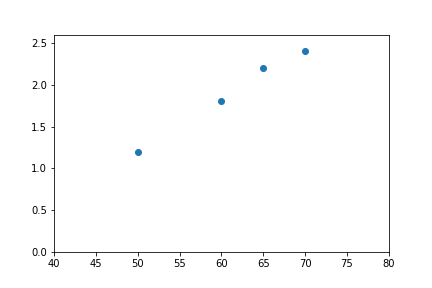
Dễ dàng nhận thấy, trong trường hợp này hàm số chúng ta cần tìm (đi qua tất cả điểm dữ liệu) sẽ rất gần với đường thẳng %y=ax+b%. Do đó, ta sẽ thử đi tìm xem có hàm %y=ax+b% nào thỏa mãn điều kiện dữ liệu hay không. Vì %y=ax+b% là một hàm số tuyến tính, cho nên phương pháp này được gọi là hồi quy tuyến tính (linear regression).
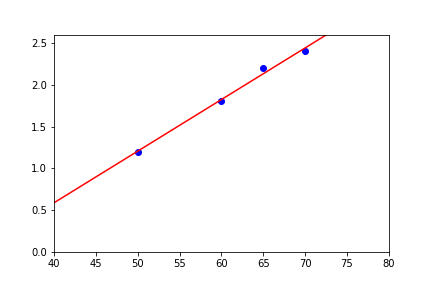
Hồi quy tuyến tính cũng có thể áp dụng ý cho miền dữ liệu đầu vào nhiều chiều hơn. Cụ thể, ta cùng thử với dữ liệu đầu vào %X \in \mathbb{R}^2% như ví dụ ban đầu.
Xây dựng hàm mục tiêu
Xét vector %X \in \mathbb{R}^{2}%, với %x_{i, 1} \in X% là diện tích căn hộ và %x_{i, 2} \in X% tương đương là số phòng của căn hộ:
$$\begin{equation}\tag{1}X=\begin{bmatrix}
60 & 2 \\
70 & 3 \\
50 & 1 \\
35 & 3
\end{bmatrix}\end{equation}$$
Tiếp tục gọi %Y=\begin{bmatrix}1.8 & 2.4 & 1.2 & 2.2 \end{bmatrix}^T% là giá trị của căn hộ. Khi đó, cần tìm %\theta% sao cho %y_i=\theta_0 + \theta_1 x_{i,1} + \theta_2 x_{i,2}%, trong đó %\theta_0% là hệ số tự do (đây là hàm tuyến tính cơ bản nhất, tương đương với hàm %y=ax+b%). Để thuận tiện cho việc tính toán, ta thêm hệ số %1% vào %x_i%, và viết dưới dạng ma trận như sau:
$$\begin{equation}\tag{2}\begin{bmatrix}1.8 \\ 2.4 \\ 1.2 \\ 2.2 \end{bmatrix}\end{equation}=\begin{bmatrix}
1 &60 & 2 \\
1 & 70 & 3 \\
1 & 50 & 1 \\
1 & 35 & 3
\end{bmatrix}\times \begin{bmatrix}\theta_0 \\ \theta_1 \\ \theta_2\end{bmatrix}$$
Ngoài ra, ta cũng có thể viết %y=h(x)=\theta x%. Như đã đề cặp ở bài trước, giá trị dự đoán sẽ có sai lệch so với giá trị mục tiêu và giá trị sai lệch đó chính là thứ cần phải cực tiểu hóa. Ở đây ta giả sử mỗi giá trị dự đoán %y_{i}^{\prime}% lệch so với giá trị mục tiêu %y_{i}% một giá trị %\epsilon_{i}%:
$$y_{i}=y_{i}^{\prime} + \epsilon_{i}\tag{3}$$
Tiếp tục giả định %\epsilon_i% phân phối độc lập và đồng nhất (independently and identically distributed) theo phân bố chuẩn (Normal distribution):
$$\epsilon_i \sim \mathcal{N}(0,\,\sigma^{2})\tag{4}$$
Như vậy, ta có hàm mật độ xác suất của %\epsilon_i%:
$$p\left(\epsilon_{i}\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(\epsilon_{i}\right)^2}{2 \sigma^2}\right)\tag{5}$$
Vì đã có %(3)% và %(4)%, cho nên ta cũng có:
$$p\left(y_{i} \mid x_{i} ; \theta\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_{i}-\theta x_{i}\right)^2}{2 \sigma^2}\right)\tag{6}$$
Trong đó %p\left(y_{i} \mid x_{i} ; \theta\right)% là xác suất có điều kiện của %y_i% theo %x_i% và bộ tham số %\theta%. Một cách tổng quát hơn ta cần tìm %p\left(y^{\prime} \mid X ; \theta\right)%, với %X% và %y^{\prime}% là hai vector chứa toàn bộ giá trị đầu vào và đầu ra tương ứng. Có thể thấy, với mỗi bộ tham số %\theta% và các giá trị đầu vào %X% cho trước thì sẽ tính ra được một %y^{\prime}% khác nhau. Do đó, ta cần tìm bộ tham số %\theta% sao cho %y^{\prime}% gần với %y% nhất. Tức là phải tìm %\theta% để cực đại hóa %p\left(y_{i} \mid x_{i} ; \theta\right)%.
Dựa vào nguyên tắc Maximum Likelihood, đầu tiên phải viết lại hàm likelihood:
$$L(\theta)=L(\theta ; X, y^{\prime})=p(y^{\prime} \mid X ; \theta)\tag{7}$$
Nhờ vào giả định độc lập và đồng nhất của dữ liệu (IID), nên %L(\theta)% có thể tính như sau (%n% là số lượng điểm dữ liệu cho trước %n=|X|%):
$$\begin{equation}\begin{aligned}L(\theta) &=\prod_{i=1}^n p\left(y_{i} \mid x_{i} ; \theta\right) \\ &=\prod_{i=1}^n \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_{i}-\theta x_{i}\right)^2}{2 \sigma^2}\right)\end{aligned}\end{equation}\tag{8}$$
Bây giờ việc cần làm là tìm %\theta% để cực đại hóa (maximize) %L(\theta)%, tức tìm %\arg \max_{\theta}L(\theta)%. Tuy nhiên, để đơn giản hơn, thay vào đó ta có thể dùng hàm %\mathcal{l(\theta)}=\log{(L(\theta))}%. Khi đó, thay vì tìm %\arg \max_{\theta}L(\theta)%, thì chúng ta tìm %\arg \max_{\theta}\ell(\theta)% (làm được điều này bởi vì %\log(x)% là một hàm đơn điệu - monotone function). Việc dùng log giúp phân tích tích thành tổng, nên quá trình tính toán sẽ dễ dàng hơn rất nhiều.
$$\begin{equation}\begin{aligned}\ell(\theta) &=\log L(\theta) \\ &=\log \prod_{i=1}^n \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_{i}-\theta x_{i}\right)^2}{2 \sigma^2}\right) \\ &=\sum_{i=1}^n \log \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_{i}-\theta x_{i}\right)^2}{2 \sigma^2}\right) \\ &=n \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^n\left(y_{i}-\theta x_{i}\right)^2\end{aligned}\end{equation}\tag{9}$$
Dễ thấy, %\ell(\theta)% là hiệu của hai thành phần:
$$\ell(\theta)=n\log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^n\left(y_{i}-\theta x_{i}\right)^2\tag{10}$$
Trong đó, số bị trừ %n\log \frac{1}{\sqrt{2 \pi} \sigma}% là một giá trị cố định. Vậy để maximize %\ell(\theta)% thì ta chỉ cần minimize số trừ %\frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^n\left(y_{i}-\theta x_{i}\right)^2%, đơn giản hóa thành minimize %\frac{1}{2} \sum_{i=1}^n\left(y_{i}-\theta x_{i}\right)^2%.
Do đó bài toán từ cực đại hóa trở thành bài toán cực tiểu hóa %\ell(\theta)%:
$$\begin{equation}\boxed{\arg\min_{\theta}\frac{1}{2} \sum_{i=1}^n\left(y_{i}-\theta x_{i}\right)^2}\end{equation}\tag{11}$$
Nhưng bước trên chính là quá trình xây dựng hàm mục tiêu một cách tự nhiên nhất cho bài toán linear regression. Trong thực tế, %\ell(\theta)=\frac{1}{2} \sum_{i=1}^n\left(y_{i}-\theta x_{i}\right)^2% là hàm mục tiêu (cost function) rất phổ biến được gọi là least-square cost function.
Sau khi đã có hàm mục tiêu %\ell(\theta)%, việc tiếp theo là tìm cách giải bài toán %(11)%. Để giải bài toán %(11)%, ta có nhiều cách. Tuy nhiên ở bài này chúng ta sẽ tìm hiểu cách đơn giản và tự nhiên nhất, đó là giải phương trình đạo hàm bằng 0.
Giải phương trình đạo hàm bằng 0
Bằng kiến thức toán học cơ bản, chúng ta có thể dễ dàng biết rằng để tìm cực trị của một hàm số thì cách đơn giản nhất là giải phương trình đạo hàm bằng 0.
Xét hàm mục tiêu %\ell(\theta)%, ta có thể viết lại %\ell(\theta)% dưới dạng ma trận như sau:
$$\begin{equation}\ell(\theta)=\frac{1}{2} \sum_{i=1}^n\left(y_{i}-\theta x_{i}\right)^2\end{equation}\tag{12}$$
$$\ell(\theta)=\frac{1}{2}\left (\begin{bmatrix}y_1 \\ \vdots \\ y_n \end{bmatrix} - \begin{bmatrix}x_1 \\ \vdots \\ x_n \end{bmatrix}\times \begin{bmatrix}\theta_0 \\ \vdots \\ \theta_2\end{bmatrix} \right)^2=\frac{1}{2}(Y-X\theta)^2\tag{13}$$
Vì ta có %z^T z=\sum_i z_i^2% với %z% là vector, nên ta có thể viết lại %\ell(\theta)% thành:
$$\ell(\theta)=\frac{1}{2}(Y-X\theta)^T(Y-X\theta)\tag{14}$$
Để tìm cực trị của %\ell(\theta)%, ta sẽ giải phương trình %\nabla_\theta l(\theta) = 0%:
$$\begin{equation}\begin{aligned}0&= \nabla_\theta \ell(\theta) \\0&=\nabla_\theta \frac{1}{2}(Y-X \theta)^T(Y-X \theta) \\0&= \frac{1}{2} \nabla_\theta (Y^TY-Y^T(X\theta)-(X\theta)^TY+(X\theta)^T(X\theta))\\0&=\frac{1}{2} \nabla_\theta\left(\theta^T\left(X^T X\right) \theta-Y^T(X \theta)-Y^T(X \theta)\right) \\0&=\frac{1}{2} \nabla_\theta\left(\theta^T\left(X^T X\right) \theta-2\left(X^T Y\right)^T \theta\right) \\0&=\frac{1}{2}\left(2 X^T X \theta-2 X^T Y\right) \\0&=X^T X \theta-X^T Y\\ \implies \theta &=(X^T X)^{-1}X^T Y\end{aligned}\end{equation}\tag{15}$$
Nhắc lại một chút về đại số tuyến tính. Với một hàm số %f:\mathbb{R}^{m\times n} \rightarrow \mathbb{R}%, tức hàm %f% ánh xạ ma trận %m\times n% sang một số thực (ví dụ như hàm %y=h(\theta)%). Thì đạo hàm của %f% theo biến %A% được định nghĩa như sau:
$$\begin{equation}\nabla_A f(A)=\frac{\partial f}{\partial A}=\left[\begin{array}{ccc}\frac{\partial f}{\partial A_{11}} & \cdots & \frac{\partial f}{\partial A_{1 n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f}{\partial A_{m 1}} & \cdots & \frac{\partial f}{\partial A_{m n}}\end{array}\right]\end{equation}$$
%\nabla_A f(A)% là ma trận Jacobian với mỗi phần tử là đạo hàm riêng của %f% tương ứng với phần tử đó trong ma trận %A%: %\frac{\partial f}{\partial A_{ịj}}%.
Ngoài ra, trong lời giải trên chúng ta sử dụng một số phép biến đổi ma trận đó là:
$$\begin{equation}a^T b = b^T a\\ \nabla_x b^T x=b \\ \nabla_x x^T Ax = 2Ax\end{equation}$$
Vậy nghiệm của bài toán chính là %\boxed{\theta =(X^T X)^{-1}X^T Y}%
Dưới đây là đoạn mã Python để kiểm chứng công thức trên:
Kết quả ta thu được là: %\theta_0 =-1.0000000000001164%, %\theta_1 = 0.04000000000000292%, %\theta_2=0.1999999999999862%.
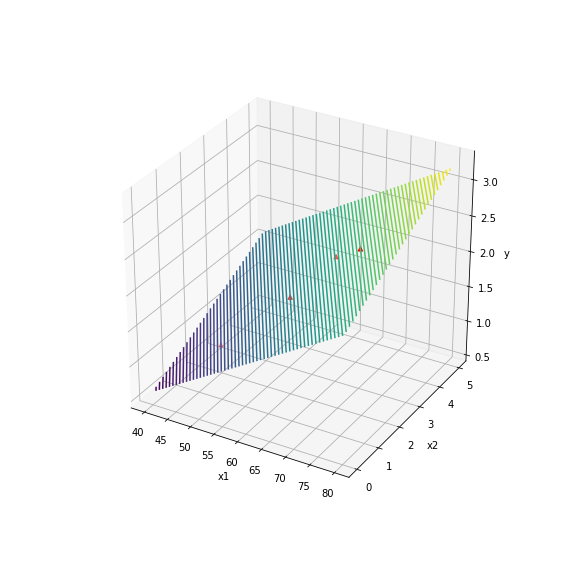
Linear regression là một mô hình đơn giản, đặc biệt nó dựa trên giả định IID của dữ liệu. Trong thực tế, các tập dữ liệu thường không bao giờ đảm bảo được tính chất độc lập và đồng nhất (IID). Cho nên linear regression áp dụng cho các tập dữ liệu phức tạp và nhiều chiều thường không mang lại kết quả tốt. Ngoài ra phương pháp giải phương trình đạo hàm bằng 0 không phải lúc nào cũng áp dụng được. Vì vậy chúng ta cần một phương pháp tối ưu khác tốt hơn. Ở bài sau, chúng ta sẽ cùng khảo sát một thuật toán tìm cực trị quan trọng của học máy đó là Gradient Descent.