ML101.03: Gradient Descent

Trong lĩnh vực tối ưu nói chung và học máy nói riêng, việc tìm cực trị của một hàm số là cực kỳ quan trọng. Như chúng ta đã biết công việc quan trọng nhất khi giải bài toán học máy đó là tìm bộ tham số để cực tiểu hóa loss function (hàm mất mát).

$$\boxed{\theta^{\star}=\arg \min_{\theta}\mathcal{L}(\theta)}\tag{1}$$

Gradient descent (GD) là một trong những thuật toán rất hiệu quả để giải các bài toán tối ưu như vậy, đặc biệt là đối với các hàm lồi (convex-function). GD dựa trên một khái niệm rất cơ bản của toán học đó là đạo hàm (derivatives). Đạo hàm là đại lượng thể hiện sự biến thiên của hàm số theo một biến nào đó. Ví dụ đạo hàm của %f(x)% theo biến %x% được ký hiệu như sau:

$$\frac{\partial f(x)}{\partial x}\tag{2}$$

Một cách hình học thì giá trị đạo hàm chính là hệ số góc đường tiếp tuyến của hàm %f(x)% tại điểm %(x, f(x))%.

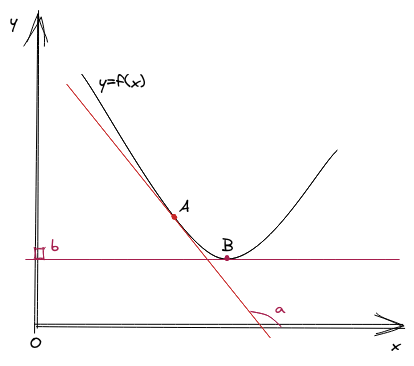
Trong hình trên, ta có ví dụ về 2 đường tiếp tuyến của %y=f(x)% tại hai điểm %A% và %B%. Tạm gọi hai giá trị đạo hàm tương ứng là %a% và %b%. Bởi vì đạo hàm của %y=f(x)% theo %x% là hệ số gốc của đường tiếp tuyến theo trục hoành %x%. Nên như trên hình, có thể thấy %a > b% và %b = 0% (vì đường tiếp tuyến đi qua điểm %B% vuông góc với trục tung %y%). Mặt khác, %b=0% thể hiện rằng đường thẳng %y=f(x)% không có "xu hướng" lên hoặc xuống tại điểm %B%. Cho nên điểm %B% chính là điểm mà hàm số đặt cực trị (extrema). Nếu như đạo hàm là một đại lượng vô hướng, thì ta có một khái niệm tổng quát hơn là gradient. Gradient là vector có hướng biểu diễn sự biến thiên của hàm số trên từng biến thành phần. Nói cách khác thì với hàm nhiều biến, gradient là vector chứa đạo hàm riêng (partial derivative) của hàm số theo từng biến của hàm đó. Gradient của %f(x)% tại điểm %p \in \mathbb{R}^n% được thể hiện như sau:

$$\nabla f(p)=\left[\begin{array}{c}
\frac{\partial f}{\partial x_1}(p) \\
\vdots \\
\frac{\partial f}{\partial x_n}(p)
\end{array}\right]\tag{3}$$

Gradient Descent

Mục tiêu của thuật toán gradient descent là từ một điểm xuất phát %A% bất kỳ, tìm cách dịch chuyển điểm %A% đến càng gần cực trị càng tốt. Ví dụ, từ điểm %A%, thuật toán có thể đi qua %A1, A2,..An% để đến %B%. Mỗi một lần di chuyển từ %A% đến %Ai% được gọi là một "bước nhảy gradient".

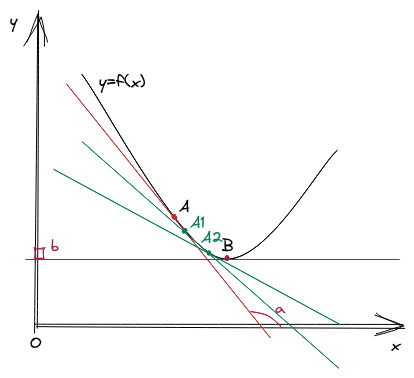
Bước nhảy gradient được thể hiện bằng công thức: %A_{n+1}=A_{n}-\alpha \nabla A_n%. Trong đó, %\alpha% là learning rate giúp điều chỉnh độ lớn của gradient tại mỗi bước nhảy. Trở lại bài toán %(1)%, nếu ta áp dụng gradient descent để tìm %\theta^{\star}% thì ta có công thức như sau:

$$\boxed{\theta_{n+1}=\theta_{n} - \alpha \nabla \mathcal{L(\theta)}}\tag{4}$$

Trong công thức trên, một điều dễ nhận thấy đó là %\mathcal{L}(\theta)% bắt buộc phải khả vi và liên tục trên miền tìm kiếm của %\theta%.

Các bước của thuật toán gradient descent:

• Bước 1: Khởi tạo %\theta%, %\alpha%.
• Bước 2: Lặp lại phép tính %\theta \leftarrow \theta - \alpha \nabla \mathcal{L}(\theta)% cho đến khi gặp phải điều kiện dừng.

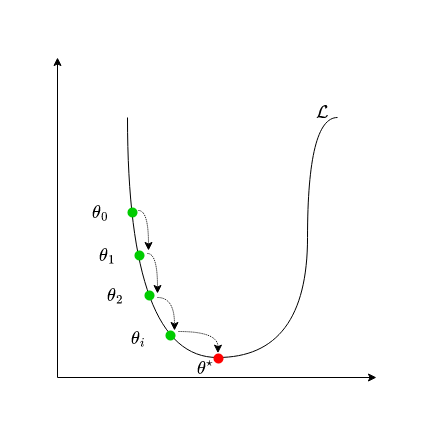
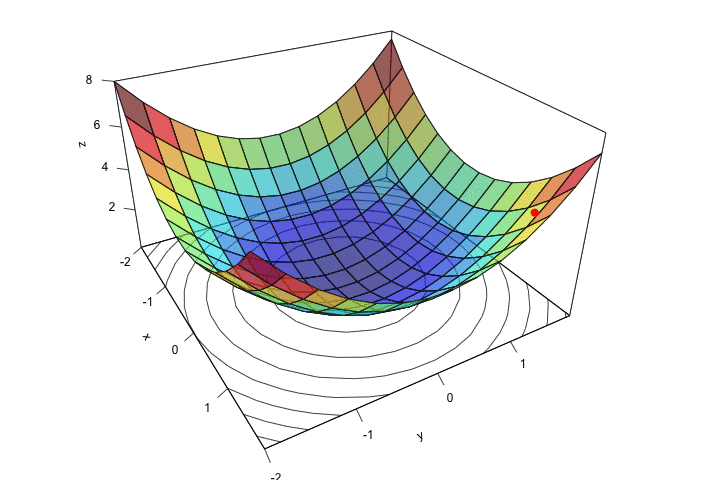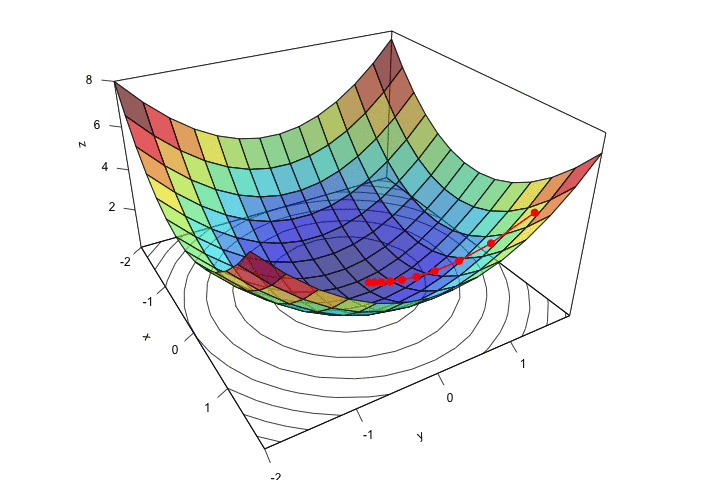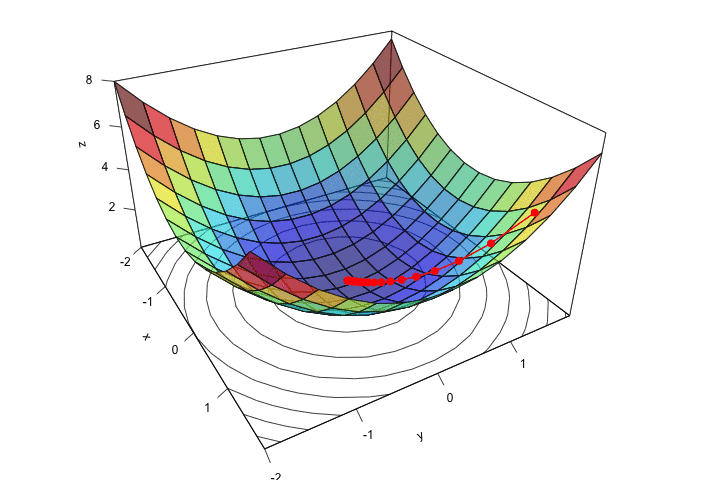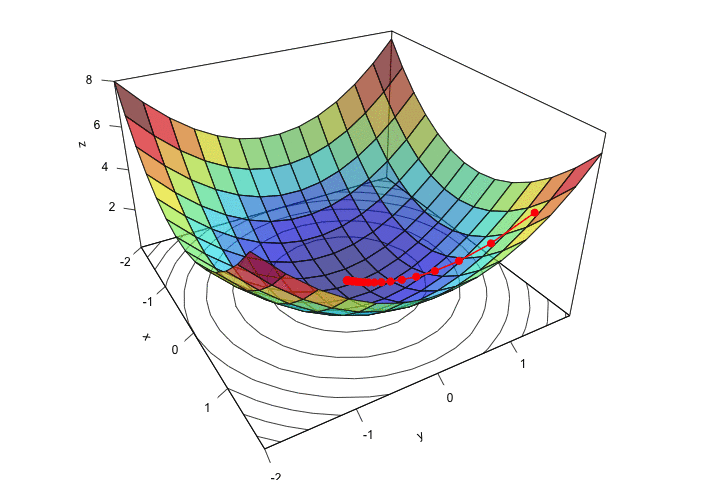
Chúng ta có thể thấy, ở bước 1 là khởi tạo %\theta% và %\alpha%. Việc khởi tạo tham số mô hình và learning rate là hết sức quan trọng. Nếu khởi tạo bộ tham số ở quá xa so với điểm global optima, hoặc khởi tạo bộ tham số ở quá gần với local optima hay saddle point thì rất khó để mô hình có thể hội tụ như ý muốn. Còn nếu khởi tạo learning rate quá nhỏ thì thuật toán sẽ hội tụ rất chậm, khi learning rate quá lớn lại có thể khiến cho thuật toán phân kì, không thể hội tụ. Tạm thời chúng ta chấp nhận khởi tạo ngẫu nhiên tham số mô hình %\theta% và dựa vào kinh nghiệm để khởi tạo learning rate %\alpha%. Chúng ta sẽ tìm hiểu sâu hơn về phương pháp khởi tạo %\theta% và %\alpha% hiệu quả ở những bài viết chi tiết hơn.

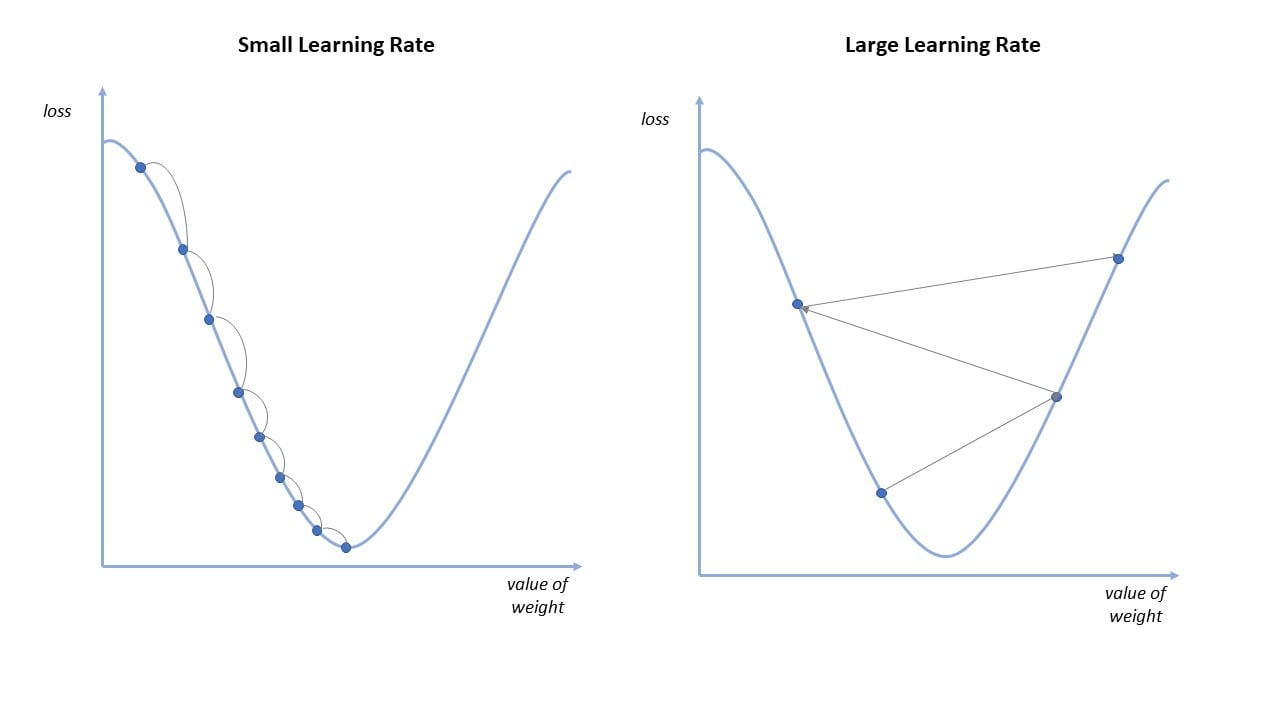
Điều kiện dừng

Ta có thể thấy, điều kiện dừng lí tưởng nhất của gradient descent là khi gradient bằng 0. Tuy nhiên, trên thực tế các hàm số thường phức tạp và rất khó để tiến để điểm cực trị. Mặt khác, không phải thuật toán gradient descent không phải lúc nào cũng hội tụ (convergence). Trong trường hợp xấu nhất, thuật toán có thể không bao giờ đến được điểm cực trị do rơi vào điểm local optima (điểm cực trị cục bộ) hoặc điểm yên ngựa (saddle point). Đây là hai trường hợp rất hay gặp khi dùng gradient descent để tìm cực trị của các hàm non-convex. Đây đều là những điểm có gradient bằng 0, nhưng lại không phải là global optima (điểm tối ưu toàn cục) mà chỉ là local optima (điểm tối ưu cục bộ). Vì vậy một khi đã rơi vào những điểm này thì rất khó để thuật toán GD có thể thoát ra. Đây cũng là một trong các điểm yếu lớn nhất của gradient descent.

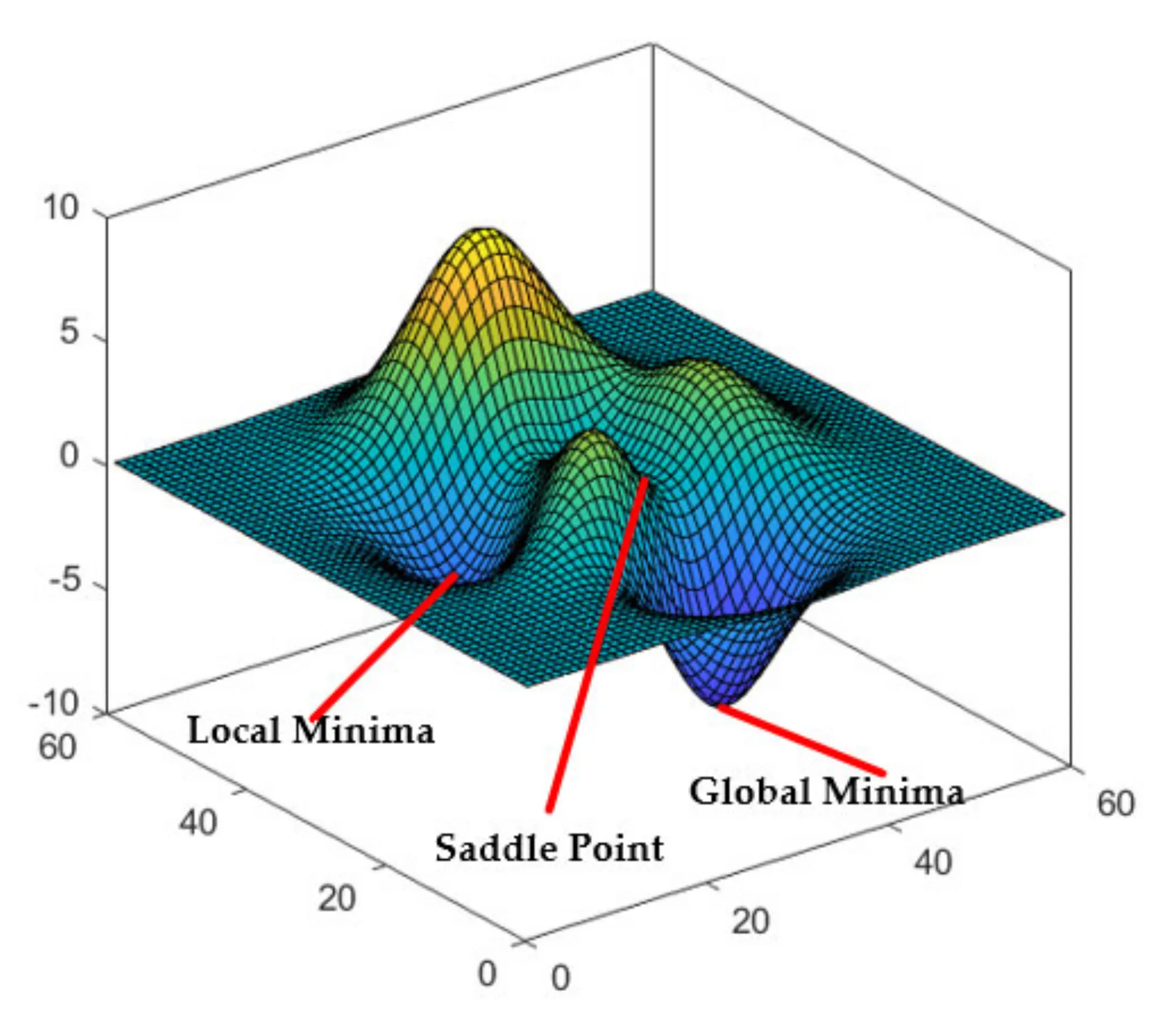
Do khả năng tính toán có hạn cho nên khi thiết kế thuật toán, chúng ta thường dùng các cách sau để làm điều kiện dừng cho gradient descent:

• Lặp với số lần lặp xác định: Đây là cách đơn giản nhất mà chúng ta có thể nghĩ tới. Chúng ta hi vọng rằng với một số lần lặp đủ nhiều nằm trong giới hạn tính toán thì thuật toán sẽ hội tụ. Đây cũng chính là cách được dùng rộng rãi nhất.
• Lặp cho đến khi đạt được tiêu chí của hàm mục tiêu: Giả sử khi bắt tay giải bài toán học máy. Chúng ta chấp nhận một sai số nhất định của giải pháp thì khi hàm mục tiêu đạt được tiêu chí này chúng ta có thể cho dừng thuật toán. Ví dụ chúng ta cần huấn luyện mô hình phân lớp với độ chính xác chấp nhận được là %99\%%. Thì khi gradient descent giúp mô hình đạt được tiêu chí này thì có thể cho dừng thuật toán. Thông thường tiêu chí của hàm mục tiêu sẽ là %\mathcal{L}(\theta) < \epsilon%, với %\epsilon% là một hằng số được người thiết kế thuật toán quy định sẵn.
• Cơ chế dừng sớm (early stopping): Cơ chế dừng sớm là giải pháp giúp gradient descent tránh được những trường hợp lặp vô hạn hoặc quá khớp (overfitting). Theo đó, nếu trong quá trình lặp mà hàm mục tiêu (loss function) không có xu hướng giảm mà ngược lại còn tăng liên tiếp thì chúng ta sẽ dừng lại. Đây cũng là một phương pháp được sử dụng khá phổ biến. Chúng ta sẽ tìm hiểu chi tiết hơn về cơ chế này ở bài viết về quá khớp và chuẩn hóa.

Các biến thể của Gradient Descent

• Batch Gradient Descent: Đối với Batch Gradient Descent việc tính toán gradient sẽ được thực hiện cho từng mẫu dữ liệu huấn luyện và được cộng lại. Sau khi đã duyệt qua toàn bộ mẫu dữ liệu huấn luyện thì thực hiện cập nhật tham số %\theta%: $$\theta_{n + 1} = \theta_n - \alpha \sum_{i=1}^N \frac{\partial \mathcal{L}(\theta)}{\partial \theta_i}\tag{5}$$ Trên thực tế, để đảm bảo tính ổn định của gradient và giá trị bước nhảy. Người ta hay dùng trung bình cộng gradient của toàn bộ batch để cập nhật dữ liệu. Do đó, công thức được viết lại như sau: $$\theta_{n + 1} = \theta_n - \frac{\alpha}{N} \sum_{i=1}^N \frac{\partial \mathcal{L}(\theta)}{\partial \theta_i}\tag{6}$$ Batch Gradient Descent giúp tối ưu bộ nhớ cần dùng để tính toán (do mỗi lần chỉ tính gradient cho một mẫu). Tuy nhiên về mặt thời gian mà nói thì lại rất chậm. Mặt khác, tuy biến thể này giúp gradient của thuật toán có phần ổn định hơn. Nhưng nó lại thường đưa mô hình đến điểm local optima hơn là global optima.
• Stochastic Gradient Descent: Biến thể thứ hai của gradient descent là Stochastic Gradient Descent. SGD là thuật toán được dùng rất phổ biến trong học máy. Ý tưởng của SGD rất đơn giản, thuật toán sẽ cập nhật tham số cho từng mẫu dữ liệu. Điều này khiến tốc độ của thuật toán Stochastic Gradient Descent còn chậm hơn cả Batch Gradient Descent. Bù lại, việc cập nhật cho từng mẫu dữ liệu giúp thuật toán có khả năng thoát khỏi local optima và tìm đến global optima tốt hơn. Tuy nhiên do từng mẫu dữ liệu đều ảnh hưởng đến thuật toán nên phương pháp này lại rất nhạy cảm với dữ liệu nhiễu (noise). $$\theta_{n + 1}=\theta_n - \alpha \frac{\partial \mathcal{L}(\theta)}{\partial \theta_i},\; \text{for every i}\tag{7}$$
• Mini-batch Gradient Descent: Mini-batch Gradient Descent là phương pháp lai giữa Batch Gradient Descent và Stochastic Gradient Descent. Mini-batch Gradient Descent cũng tính gradient cho từng mẫu. Tuy nhiên, thay vì tham số được cập nhật sau khi duyệt qua toàn bộ dữ liệu huấn luyện thì Mini-batch Gradient Descent thực hiện cập nhật tham số theo từng batch dữ liệu. Ví dụ dữ liệu có 1000 mẫu và batch_size là 10, thì ta có tổng cộng 100 batch. Vì vậy mỗi lần huấn luyện, thuật toán sẽ thực hiện cập nhật tham số 100 lần tương ứng với gradient của 100 batch. Tương tự như batch gradient descent, mini-batch gradient descent cũng thường xuyên sử dụng trung bình cộng gradient để cập nhật tham số.

Polyak's Heavy Ball (Momentum)

Về cơ bản, chúng ta có thể tưởng tượng thuật toán gradient descent giống như việc thả một hòn đá lăn từ ngọn núi xuống dưới. Thung lũng sâu nhất chính là global optima cần tìm. Theo mô hình vật lý cổ điển của Newton, ta biết rằng trong quá trình di chuyển hòn đá sẽ tạo ra một quán tính nhất định. Đây là điều giúp cho hòn đá có thể từ thung lũng leo lên lại đỉnh và trượt qua nơi khác. Tuy nhiên, trong công thức của gradient descent thì chưa có đại lượng nào thể hiển lực quán tính này. Do đó Polyak [1] đã đề xuất viết lại công thức cập nhật tham số như sau:

$$\theta_{n + 1} = \theta_n - \alpha \nabla \mathcal{L}(\theta) + \beta (\theta_{n} - \theta_{n - 1})\tag{8}$$

Trong đó, %\beta (\theta_{n} - \theta_{n - 1})% chính là phần biễu diễn lực quán tính. Đó là hiệu của vector %\theta_n% và %\theta_{n-1}%. Đây là một biến thể rất hay được sử dụng của gradient descent. Polyak's heavy ball cho phép thuật toán có thể thoát khỏi các local optima và saddle point khá hiệu quả.

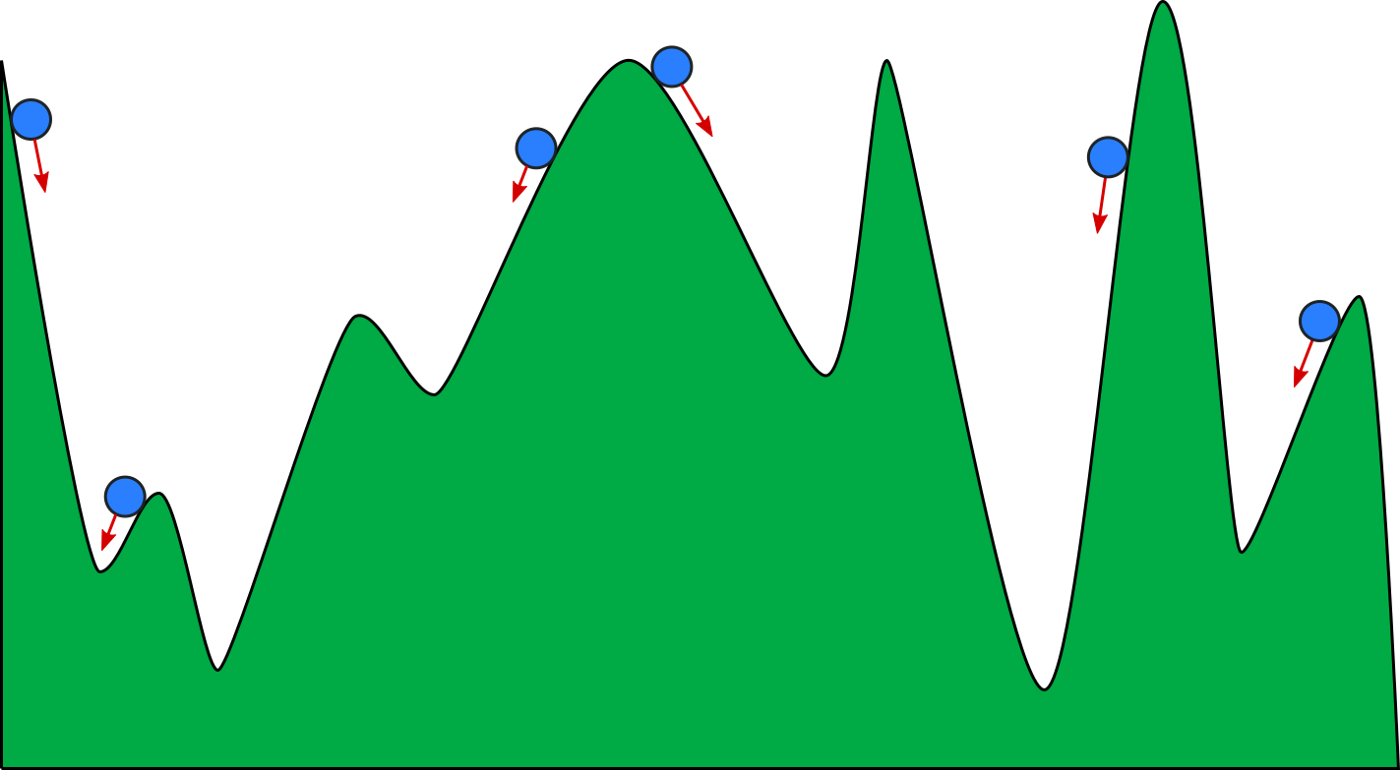
Momentum tuy giúp mô hình có thể thoát khỏi local optima, nhưng phương pháp này lại khiến cho thuật toán hội tụ chậm hơn. Lí do là bởi vì dù có đến được điểm thấp nhất của thung lũng thì hòn đá vẫn không dừng lại mà dao động xung quanh thêm một thời gian do lực quán tính. Vì vậy có nhiều phương pháp khác để tiếp tục cải tiến thuật toán này. Bạn đọc có thể tìm kiếm một số từ khóa như Nesterov's accelerated method, Adagrad, Adadelta,.. Chúng ta sẽ tìm hiểu chi tiết hơn khi áp dựng từng phương pháp tối ưu ở bài toán cụ thể.

Trên đây là một giới thiệu sơ lược về ý tưởng của gradient descent. Tuy đơn giản nhưng gradient descent chính là xương sống của rất nhiều đột phá quan trọng trong học máy. Việc nắm vững thuật toán này là một bước rất quan trọng để hiểu và vận dụng chúng vào các bài toán thực tế.

Tài liệu tham khảo

[1] Polyak, Boris T. “Some methods of speeding up the convergence of iteration methods.” USSR Computational Mathematics and Mathematical Physics 4, no. 5 (1964): 1-17.

[2] Gradient Descent - IBM Cloud Education.

[3] CS229 Lecture Notes.