ML101.09: Kernel Methods & Support Vector Machine

Kernel methods là một nhóm kỹ thuật trong học máy, được sử dụng để giải quyết các bài toán phân loại, hồi quy và phân cụm. Chúng được phát triển dựa trên ý tưởng biến đổi dữ liệu từ không gian đầu vào ban đầu sang một không gian đặc trưng mới thông qua hàm kernel, giúp cho việc học và dự đoán trở nên dễ dàng hơn. Trong phần này, chúng ta sẽ tìm hiểu về các khái niệm cơ bản của kernel methods, ý nghĩa toán học đằng sau các thuật toán và các ứng dụng của chúng trong học máy.

Hàm kernel và không gian đặc trưng

Một hàm kernel là một hàm đo độ tương đồng giữa hai điểm dữ liệu %x% và %y%. Hàm kernel được biểu diễn dưới dạng:

$$\begin{equation}K(x, y)=\langle\phi(x), \phi(y)\rangle\end{equation}$$

Trong đó, %\phi% là hàm ánh xạ từ không gian đầu vào sang không gian đặc trưng và %\langle \cdot, \cdot \rangle% là tích vô hướng giữa hai vector. Hàm kernel thường được chọn sao cho nó thỏa mãn điều kiện Mercer, tức là ma trận kernel phải là ma trận bán xác định dương. Điều kiện Mercer đảm bảo rằng hàm kernel có thể được biểu diễn dưới dạng tích vô hướng của hai hàm ánh xạ %\phi%.

Một số hàm kernel phổ biến bao gồm:

• Kernel tuyến tính: %K(x, y) = \langle x, y \rangle%
• Kernel đa thức: %K(x, y) = (\langle x, y \rangle + c)^d%, với %c% và %d% là các hằng số.
• Radial basis function kernel (RBF): %K(x, y) = e^{-\frac{| x - y |^2}{2 \sigma^2}}%, với %\sigma% là độ rộng của hàm kernel.
• Kernel Sigmoid: %K(x, y) = \tanh(\alpha \langle x, y \rangle + c)%, với %\alpha% và %c% là các hằng số.

Hàm kernel có thể được hiểu là một cầu nối giữa không gian đầu vào và không gian đặc trưng, giúp biến đổi dữ liệu từ không gian đầu vào ban đầu sang một không gian đặc trưng mới, nơi mà các mẫu dữ liệu có thể được phân tách dễ dàng hơn. Hàm kernel giúp giảm thiểu chi phí tính toán khi chúng ta không cần biết hàm ánh xạ %\phi% mà chỉ cần biết giá trị của tích vô hướng giữa các điểm dữ liệu sau khi ánh xạ. Điều này cho phép chúng ta giải quyết các bài toán không tuyến tính mà không cần tìm ra hàm ánh xạ tường minh.

Phương pháp học dựa trên Kernel

Phương pháp học dựa trên kernel là việc sử dụng các hàm kernel để biến đổi dữ liệu và giải quyết các bài toán trong học máy. Các thuật toán phổ biến trong phương pháp học dựa trên kernel bao gồm:

• Máy vector hỗ trợ (SVM)
• Kernel Ridge Regression (KRR)
• Gaussian Process Regression (GPR)
• Kernel Principal Component Analysis (KPCA)
• Kernel K-means

Máy vector hỗ trợ (SVM)

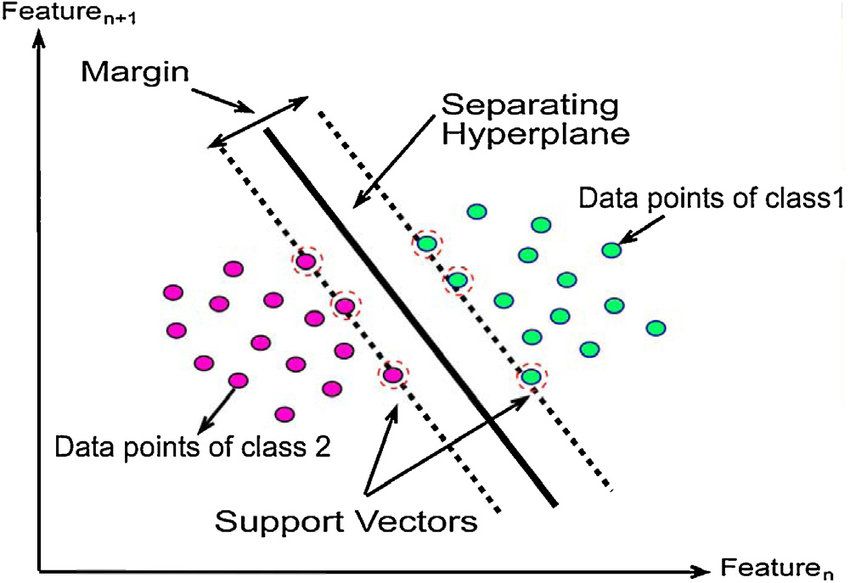
Máy vector hỗ trợ (Support Vector Machine) là một phương pháp phân loại tuyến tính dựa trên việc tìm đường biên phân chia (decision boundary) có margin lớn nhất giữa các lớp dữ liệu. Trong trường hợp dữ liệu không tuyến tính, chúng ta có thể sử dụng kernel SVM để biến đổi dữ liệu sang không gian đặc trưng mới và tìm đường biên phân chia trong không gian đó.

Bài toán tối ưu trong kernel SVM được biểu diễn dưới dạng:

$$\begin{equation} \min _{\mathbf{w}, b, \boldsymbol{\xi}} \frac{1}{2}\|\mathbf{w}\|^2+C \sum_{i=1}^N \xi_i \end{equation}$$

với ràng buộc:

$$\begin{equation}y_i\left(\left\langle\mathbf{w}, \phi\left(\mathbf{x}_i\right)\right\rangle+b\right) \geq 1-\xi_i, \quad \xi_i \geq 0, \quad i=1, \ldots, N\end{equation}$$

Trong đó, %\mathbf{w}% là vector trọng số, %b% là bias, %\boldsymbol{\xi}% là biến slack, %C% là tham số điều chỉnh và %N% là số điểm dữ liệu.

Bằng cách giải bài toán tối ưu trên, chúng ta có thể tìm ra các vector hỗ trợ (support vectors) và đường biên quyết định giữa các lớp dữ liệu. Mức độ phức tạp của kernel SVM phụ thuộc vào số lượng vector hỗ trợ, chứ không phải số chiều của không gian đặc trưng, giúp giảm chi phí tính toán trong nhiều trường hợp.

Kernel Ridge Regression (KRR)

Kernel Ridge Regression (KRR) chính là phương pháp sử dụng Ridge Regression nhưng được kế hợp thêm với kỹ thuật dùng kernel để biến đổi dữ liệu đầu vào.

Bài toán tối ưu trong KRR được biểu diễn dưới dạng:

$$\begin{equation}\min _{\boldsymbol{\alpha}} \frac{1}{2} \sum_{i=1}^N\left(y_i-\sum_{j=1}^N \alpha_j K\left(\mathbf{x}_i, \mathbf{x}_j\right)\right)^2+\frac{\lambda}{2} \boldsymbol{\alpha}^T \mathbf{K} \boldsymbol{\alpha}\end{equation}$$

Trong đó, %\boldsymbol{\alpha}% là vector hệ số, %\lambda% là tham số điều chỉnh, %\mathbf{K}% là ma trận kernel và %N% là số điểm dữ liệu.

Giải bài toán tối ưu này, chúng ta có thể tìm được hệ số %\boldsymbol{\alpha}% để dự đoán giá trị đầu ra của các điểm dữ liệu mới dựa trên độ tương đồng giữa chúng và các điểm dữ liệu trong tập huấn luyện.

Gaussian Process Regression (GPR)

Gaussian Process Regression (GPR) là một phương pháp hồi quy không tham số mạnh mẽ dựa trên khái niệm về Gaussian Processes (GP). GPR cho phép xác định mối quan hệ không tuyến tính giữa các biến đầu vào và đầu ra, đồng thời đưa ra phương sai cho dự đoán, giúp đánh giá độ không chắc chắn của mô hình.

Một Gaussian Process là một phân phối xác suất trên không gian hàm số, trong đó mỗi điểm của không gian đầu vào được ánh xạ vào một giá trị đầu ra với phân phối Gaussian. Một GP được định nghĩa bởi hàm kỳ vọng (mean function) và hàm hiệp phương sai (covariance function) của quá trình. Trong bài toán GPR, chúng ta thường giả định hàm kỳ vọng bằng 0 và sử dụng hàm hiệp phương sai được xây dựng từ một hàm kernel.

Các bước chính của GPR:

1. Chọn một hàm kernel: Chọn một hàm kernel phù hợp để xây dựng ma trận hiệp phương sai giữa các điểm dữ liệu. Hàm kernel thường được sử dụng là RBF (Radial Basis Function) kernel, Matérn kernel, hoặc Polynomial kernel.
2. Tính toán ma trận hiệp phương sai: Xây dựng ma trận hiệp phương sai giữa các điểm dữ liệu trong tập huấn luyện và giữa tập huấn luyện và tập kiểm tra.
3. Tính toán giá trị dự đoán và phương sai: Dựa vào ma trận hiệp phương sai, tính toán giá trị dự đoán và phương sai cho các điểm trong tập kiểm tra

Kernel Principal Component Analysis (KPCA)

Kernel Principal Component Analysis (KPCA) là một phương pháp giảm chiều dữ liệu dựa trên phân tích thành phần chính (PCA) trong không gian đặc trưng được ánh xạ qua hàm kernel. KPCA giúp chúng ta tìm ra các thành phần chính không tuyến tính của dữ liệu và biến đổi chúng sang một không gian con ít chiều hơn.

Để thực hiện KPCA, chúng ta cần xây dựng ma trận kernel %\mathbf{K}% và chuẩn hóa nó bằng cách trừ đi giá trị trung bình của mỗi hàng và cột. Sau đó, chúng ta tính toán các giá trị riêng và vector riêng của ma trận kernel chuẩn hóa, và sắp xếp chúng theo thứ tự giảm dần của giá trị riêng. Cuối cùng, chúng ta chọn %k% vector riêng tương ứng với %k% giá trị riêng lớn nhất để biến đổi dữ liệu sang không gian con %k% chiều.

Kernel K-means

Kernel K-means là một phương pháp phân cụm dựa trên thuật toán K-means trong không gian đặc trưng được ánh xạ qua hàm kernel. Kernel K-means giúp chúng ta phân cụm dữ liệu không tuyến tính và tìm ra các cụm dữ liệu có hình dạng phức tạp.

Để thực hiện Kernel K-means, chúng ta cần xây dựng ma trận kernel %\mathbf{K}% và khởi tạo các nhãn cụm ngẫu nhiên cho các điểm dữ liệu. Sau đó, chúng ta lặp lại các bước sau đây cho đến khi hội tụ:

• Tính toán trung tâm của mỗi cụm trong không gian đặc trưng bằng cách sử dụng hàm kernel.
• Cập nhật nhãn cụm cho mỗi điểm dữ liệu dựa trên trung tâm cụm gần nhất.

Cuối cùng, chúng ta thu được phân cụm của dữ liệu trong không gian đặc trưng và có thể áp dụng kết quả này cho việc phân loại hoặc giảm chiều dữ liệu.

Ví dụ

Trước tiên, hãy tạo dữ liệu mô phỏng cho bài toán phân loại và hồi quy. Để đơn giản, chúng ta sẽ sử dụng dữ liệu 2D và tạo dữ liệu không tuyến tính. Sau đó, ta sẽ sử dụng thư viện scikit-learn để hiện thực các thuật toán trên:

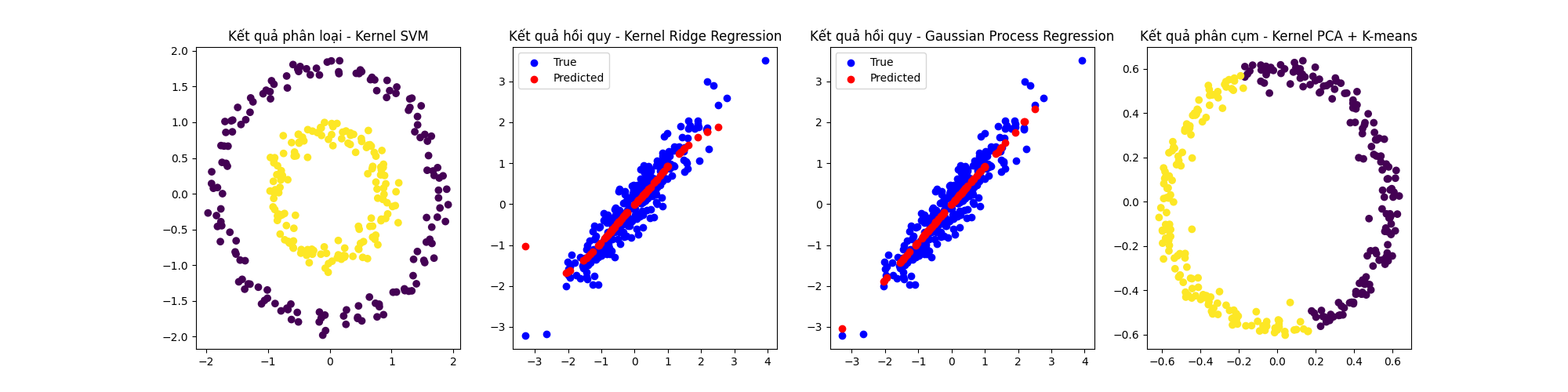
Sau khi chạy đoạn mã trên, ta được một kết quả ví dụ như sau:

Accuracy của Kernel SVM: 1.0
MSE của Kernel Ridge Regression: 0.18242662662240225
MSE của Gaussian Process Regression: 0.12085005734436872
Accuracy của Kernel PCA + K-means: 0.5

• Accuracy của Kernel SVM: Độ chính xác của Kernel SVM vẫn là 1.0 (100%). Điều này cho thấy thuật toán đã hoạt động rất tốt trong việc phân loại dữ liệu không tuyến tính trong bộ dữ liệu phân loại mô phỏng. Kernel SVM đã học được đường biên quyết định phân loại chính xác giữa hai lớp.
• MSE của Kernel Ridge Regression: Giá trị MSE (Mean Squared Error) của Kernel Ridge Regression vẫn là 0.1824. Đây là một giá trị khá thấp, cho thấy mô hình hồi quy đã học khá tốt mối quan hệ không tuyến tính giữa đặc trưng đầu vào và đầu ra trong bộ dữ liệu hồi quy mô phỏng.
• MSE của Gaussian Process Regression: Giá trị MSE của Gaussian Process Regression giờ đã giảm xuống còn 0.1209, đây là một giá trị thấp hơn so với Kernel Ridge Regression. Điều này cho thấy mô hình Gaussian Process Regression đã cải thiện đáng kể và hoạt động tốt trong bài toán hồi quy không tuyến tính này. Có thể là do việc sử dụng kernel và tham số phù hợp hơn.
• Accuracy của Kernel PCA + K-means: Độ chính xác của việc kết hợp Kernel PCA và K-means là 0.5 (50%). Điều này cho thấy phương pháp này chưa hoạt động tốt trong việc phân cụm dữ liệu không mô phỏng. Có thể là do việc chọn kernel hoặc số lượng thành phần chính (n_components) chưa phù hợp.

Nhìn chung, Kernel SVM, Kernel Ridge Regression và Gaussian Process Regression đều hoạt động tốt trong các bài toán phân loại và hồi quy không tuyến tính với dữ liệu mô phỏng. Tuy nhiên, kết hợp Kernel PCA + K-means vẫn chưa cho kết quả tốt trong việc phân cụm dữ liệu mô phỏng.

Kết

Kernel methods là một nhóm kỹ thuật hữu ích trong học máy, giúp giải quyết các bài toán phân loại, hồi quy và phân cụm không tuyến tính. Chúng được sử dụng rộng rãi trong nhiều lĩnh vực và ứng dụng thực tế như nhận dạng khuôn mặt, phân tích ngôn ngữ tự nhiên, dự đoán chuỗi thời gian và nhiều lĩnh vực khác. Bằng cách sử dụng các hàm kernel để ánh xạ dữ liệu sang không gian đặc trưng mới, kernel methods giúp chúng ta tận dụng tính toán hiệu quả của tích vô hướng giữa các điểm dữ liệu sau khi ánh xạ, thay vì cần tìm ra hàm ánh xạ tường minh.

Các thuật toán phổ biến trong kernel methods bao gồm máy vector hỗ trợ (SVM), Kernel Ridge Regression (KRR), Gaussian Process Regression (GPR), Kernel Principal Component Analysis (KPCA) và Kernel K-means. Mỗi thuật toán có những đặc điểm và ứng dụng riêng, tùy thuộc vào bài toán và loại dữ liệu đang xử lý.

Trong tương lai, kernel methods có thể được kết hợp với các kỹ thuật học máy khác như mạng nơ-ron sâu (deep neural networks) và học tăng cường (reinforcement learning) để giải quyết các bài toán phức tạp hơn và đạt được hiệu suất cao hơn. Ngoài ra, việc phát triển các hàm kernel mới và tối ưu hóa thuật toán cũng sẽ giúp cải thiện hiệu quả của kernel methods và mở ra nhiều cơ hội ứng dụng mới.

Như vậy, chúng ta đã tìm hiểu sâu hơn về kernel methods, các thuật toán trong nhóm này, cũng như những ứng dụng thực tế của chúng.