ML101.05: Softmax Regression

Đối với các bài toán phân lớp nhị phân (binary classifier) thì ta đã biết được một phương pháp giải quyết đó là Logistic Regression. Vậy với các bài toán phân lớp có nhiều lớp hơn thì sao? Trong thực thế có rất nhiều bài toán như vậy. Ví dụ như bài toán phân loại sản phẩm trong thương mại điện tử. Bài toán được mô tả như sau: cho thông tin của một sản phẩm bất kỳ và xác định xem sản phẩm đó thuộc loại nào. Có thể thấy, khác với bài toán phân lớp nhị phân, bài toán này có số lượng nhãn lớn hơn %2% và có thể là rất nhiều nhãn. Do đó ta cần một cách khác để giải quyết những bài toán phân loại đa lớp như vậy (multi-class classification).
Một cách tổng quát, ta mô hình hoá bài toán thành tìm hàm số %y=f(x)%, với %x \in \mathbb{R}^d% và %y \in \{1, 2, 3,..,k\}% sao cho thoả mãn những điểm dữ liệu %\{(x_1, y_1), (x_2, y_2),.. , (x_n, y_n)\}%. Nếu như với Logistic Regression chúng ta đi tìm xác suất rơi vào một trong hai nhãn %0% và %1%. Thì ở bài toán này chúng ta phải tìm xác suất của %k% nhãn. Do đó, %y% thay vì là một giá trị xác suất trong đoạn %[0, 1]%, thì ta cần phải có %k% giá trị đại diện cho xác suất rơi vào từng nhãn trong %k% nhãn đã cho. Vì vậy %y% là một vector với %k% chiều hay %y \in \mathbb{R}^k%. Nếu coi %y_i% là xác xuất mẫu dữ liệu %x% rơi vào nhãn %i% thì sau khi có được %y% chúng ta chỉ cần tìm xem nhãn nào có xác xuất cao nhất và xem đó là kết quả dự đoán. Ý tưởng này có thể dễ dàng thực hiện bằng cách sử dụng sigmoid function cho %k% giá trị đầu ra.
Tuy nhiên nếu làm như vậy thì chẳng khác nào chúng ta huấn luyện %k% mô hình Logistic Regression khác nhau và %k% nhãn này sẽ không hề có sự liên quan gì với nhau về mặt dự đoán. Liệu có một cách nào khác giúp ràng buộc chặt chẽ hơn giá trị đầu ra hay không?
Dễ nhận thấy, vì chỉ quan tâm đến việc so sánh các giá trị xác suất với nhau. Cho nên ta có thể đặt điều kiện tổng bằng %1% cho tất cả các giá trị xác suất này. Khi đó, bài toán trở thành tìm phân bố xác xuất %p(y \mid X; \theta)% thỏa mãn %\{(x_1, y_1), (x_2, y_2),.. , (x_n, y_n)\}%. Đây là cách tiếp cận tự nhiên hơn rất nhiều.
$$p(y=0\mid X; \theta)+p(y=1\mid X; \theta)+..+p(y=k-1\mid X; \theta)=\sum_{i}^{k}p(y\mid X; \theta)=1\tag{1}$$
Với cách viết này, ta thấy nhãn đúng (ground-truth target) được thể hiện bằng các vector one-hot %T(x) \in \{0, 1\}^k% như sau:
$$T(0)=\left[\begin{array}{c}
1 \\
0 \\
0 \\
\vdots \\
0
\end{array}\right], T(1)=\left[\begin{array}{c}
0 \\
1 \\
0 \\
\vdots \\
0
\end{array}\right], \cdots, T(k-1)=\left[\begin{array}{c}
0 \\
0 \\
0 \\
\vdots \\
1
\end{array}\right]$$
Còn nhãn dự đoán %y \in (0, 1)^k% cho điểm dữ liệu %x% thì được thể hiện như sau:
$$y=\left[\begin{array}{c}
p(y=0\mid x; \theta) \\
p(y=1\mid x; \theta) \\
p(y=2\mid x; \theta) \\
\vdots \\
p(y=k\mid x; \theta)
\end{array}\right]$$
Vậy làm thế nào để có được vector đầu ra %y \in (0, 1)^k% như trên? Lưu ý vì giá trị đầu ra của bài toán ngầm định là một giá trị xác suất, nên ngoài đảm bảo được điều kiện %(1)% thì nó còn phải không âm. Trên thực tế, những hàm đáp ứng được các điều kiện trên rất nhiều. Ví dụ như hàm:
$$p(y=i\mid x; \theta)=e^{\theta_i x}\tag{2}$$
Có thể thấy %e^{\theta_i x}% sẽ không bao giờ trả về giá trị âm, và thêm nữa nó là một hàm đồng biến (%\theta_i x% tăng thì %e^{\theta_i x}% cũng tăng). Do đó đây là một hàm số tuyệt vời để mô hình hoá giá trị xác suất. Tuy nhiên, còn điều kiện tổng bằng 1 thì sao. Để giải quyết vấn đề này, chúng ta cần thực hiện một kỹ thuật được gọi là chuẩn hoá. Nói đơn giản hơn đó là lấy %e^{\theta_i x}% chia cho tổng của tất cả các giá trị thành phần của vector đầu ra. Khi đó ta được công thức như bên dưới:
$$p(y=i\mid x; \theta)=\frac{e^{\theta_i x}}{\sum_{j=1}^K e^{\theta_j x}},\; \text{với}\; i =1,..,K\tag{3}$$
Đây được gọi là hàm softmax, một công thức rất nổi tiếng dùng để mô hình hoá các phân bố xác suất rời rạc. Hàm softmax được lấy ý tưởng từ vật lý và được phát biểu bởi Gibbs (1902) trong quyển textbook của mình. Trước đó, Boltzmann đã dùng phương pháp tương tự để mô hình hoá trạng thái năng lượng của phân tử được gọi là Boltzmann distribution [1, 2].
Hàm softmax %\sigma: \mathbb{R}^K \rightarrow(0,1)^K%, khi %K>1% được định nghĩa như sau:
$$\sigma(z_i)=\frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}},\; \text{với}\; i =1,..,K\tag{4}$$
Áp dụng hàm softmax cho bộ phân lớp, ta có:
$$p(y=i\mid x; \theta)=\frac{e^{\theta_i x}}{\sum_j^K{e^{\theta_j x}}}\tag{5}$$
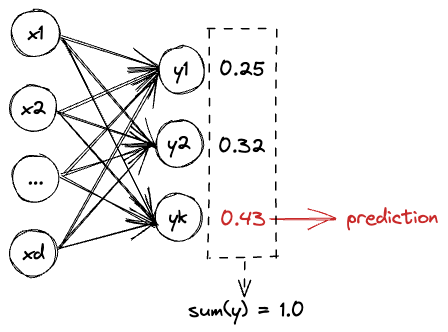
Xây dựng hàm mục tiêu
Sau khi đã xác định được mô hình tham số, như thường lệ, việc tiếp theo đó chính là xây dựng hàm mục tiêu cho mô hình đó. Đầu tiên ta xét trường hợp chỉ có một mẫu dữ liệu. Lúc này ta có %y \in \{0, 1\}^k% và %y^{\prime} \in (0, 1)^k% lần lượt là các giá trị xác suất mục tiêu và giá trị xác xuất dự đoán. Chú ý %y% ở đây được gọi là hard label vì đó là one-hot vector có dạng %[0, 0, .., 1,.., 0]^T%, còn %y^{\prime}% được gọi là soft label vì các giá trị của %y^{\prime}% mượt (smooth) hơn. Tương tự ta có %p^{\star}% là phân bố tối ưu cần tìm, còn %p% là phân bố dự đoán. Chúng ta có công thức likelihood của một mẫu dữ liệu như sau:
$$\begin{aligned}\ell(\theta) &=\prod_{l=1}^k p(y=k \mid x; \theta) \\&=\prod_{l=1}^k(y^{\prime (l)})^{1\left\{y^{(l)}=1\right\}}\end{aligned}\tag{6}$$
Trong đó, phần luỹ thừa %1\{y^{(l)}=1\}% làm indicator function, nếu điều kiện trong "{}" là đúng thì indicator function này sẽ trả về %1% và ngược lại là %0%.
Suy ra công thức likelihood cho toàn bộ dữ liệu sẽ là:
$$\ell(\theta) = \prod_{i=1}^{n} \prod_{l=1}^k (y_i^{\prime (l)})^{1\{y^{(l)}_{i}=1\}}\tag{7}$$
Tương tự như Logistic Regression, chúng ta tiếp tục đi maximize likelihood của %p(y\mid x;\theta)%:
$$\begin{aligned}\theta^{\star} &=\arg \max_{\theta}\ell(\theta) \\ &=\arg \max_{\theta}\prod_{i=1}^{n} \prod_{l=1}^k (y_i^{\prime (l)}) ^{1\{y^{(l)}_{i}=1\}} \\ &=\arg \max_{\theta}\prod_{i=1}^{n} \prod_{l=1}^k (y_i^{\prime (l)}) ^{y^{(l)}_i}\end{aligned}\tag{8}$$
Tiếp tục phân tích tích thành tổng bằng hàm log:
$$\begin{aligned}\theta^{\star} &=\arg \max_{\theta}\log(\ell(\theta)) \\ &=\arg \max_{\theta}\sum_{i=1}^{n} \sum_{l=1}^k y_i^{(l)} \log{y^{\prime (l)}_i}\end{aligned}\tag{9}$$
Bây giờ thay vì tiếp tục sử dụng công thức này để tối ưu, ta sẽ biến đổi bài toán từ maximize thành minimize bằng cách thêm dấu trừ vào hàm likelihood:
$$\boxed{\begin{aligned}\theta^{\star} &=\arg \max_{\theta}\log(\ell(\theta)) \\ &=\arg \min_{\theta}-\sum_{i=1}^{n} \sum_{l=1}^k y_i^{(l)} \log{y^{\prime (l)}_i}\end{aligned}}\tag{10}$$
Công thức %(10)% được gọi là negative log-likelihood (NLL). NLL là công thức được dùng rất nhiều cho các bài toán phân lớp. Đặc biệt, nếu ta chỉ xét loss cho một mẫu dữ liệu riêng biệt, ta có công thức cross-entropy dưới dạng rời rạc như sau:
$$\boxed{H(y, y')=-\sum_{l=1}^k y^{(l)} \log{y^{\prime (l)}}}\tag{11}$$
Trong lý thuyết thông tin, cross-entropy của hai phân phối xác suất %p%, %q% được định nghĩa như sau bởi %H(p, q)%:
$$H(p, q)=-\mathrm{E}_p[\log q]\tag{12}$$
Cross-entropy được ngầm hiểu là công thức đo "khoảng cách" giữa hai phân bố xác suất. Trên thực tế NLL và cross-entropy được hiểu và hiện thực giống nhau trong hầu hết các bài toán phân lớp (bởi vì dữ liệu đầu ra luôn rời rạc). Chúng ta sẽ đi vào chi tiết mối liên hệ giữa hai hàm loss này sau. Bây giờ sau khi đã có hàm mục tiêu, chúng ta chuyển sang bước cuối cùng đó là tối ưu hàm mục tiêu này.
Tối ưu
Cũng như các thuật toán khác, để tối ưu Softmax Regression, trước hết chúng ta phải tìm được gradient của hàm mục tiêu. Thật thú ví khi cross-entropy cho ta một công thức tính gradient rất đẹp:
$$\nabla_{\theta} H(y, y^{\prime})=(y^{\prime}-y)x\tag{13}$$
Phần chứng minh công thức trên bạn đọc có thể tham khảo tại đây.
Sau khi đã có được gradient thì ta hoàn toàn có thể bất kì thuật toán nào tương tự như Gradient Descent hay Newton's Method. Ví dụ với Gradient Descent, ta có công thức cập nhật trong số như bên dưới:
$$\theta_{n+1}:=\theta_{n} - \alpha (\theta x - y)x\tag{14}$$
Trong đó, ta thay %y^{\prime} = \theta x%.
Nhớ lại công thức maximize log-likelihood của Logistic Regression ở bài trước, ta dễ dàng nhận ra nếu dùng dấu "-" để biến đổi hàm mục tiêu của Logistic Regression thành negative log-likelihood, thì công thức cập nhật Gradient Descent cũng đổi dấu theo. Do vậy, nó trùng khớp với công thức cập nhật của Softmax Regression ở bài này. Điều này hoàn toàn không phải là sự trùng hợp. Cả Logistic Regression và Softmax Regresison đều là thành viên của một lớp các mô hình lớn được gọi là Generalized Linear Model. Tất cả các mô hình thuộc họ hàng GLM đều có thể được giải quyết thông phương pháp minimize log-likelihood với công thức gradient như trên.
Tài liệu tham khảo
[1] Gibbs, Josiah Willard (1902). Elementary Principles in Statistical Mechanics.
[2] Boltzmann, Ludwig (1868). "Studien über das Gleichgewicht der lebendigen Kraft zwischen bewegten materiellen Punkten" [Studies on the balance of living force between moving material points]. Wiener Berichte. 58: 517–560.