How Computers Generate Random Numbers
Imagine this: you're playing your favorite video game, and an enemy drops a rare item. Or maybe you're shuffling your Spotify playlist, wondering how it picks the next song. Behind these everyday moments lies a fascinating paradox: how do computers, which are fundamentally deterministic machines, create randomness?
The Not-So-Random Truth
Here's something that might surprise you: computers can't actually generate truly random numbers. These incredible machines that power our digital world are, at their core, following precise instructions step by step. What we call "random numbers" in programming are actually "carefully crafted sequences that look random" - we call them pseudorandom numbers in tech-speak.
Pseudorandom Number Generators (PRNGs)
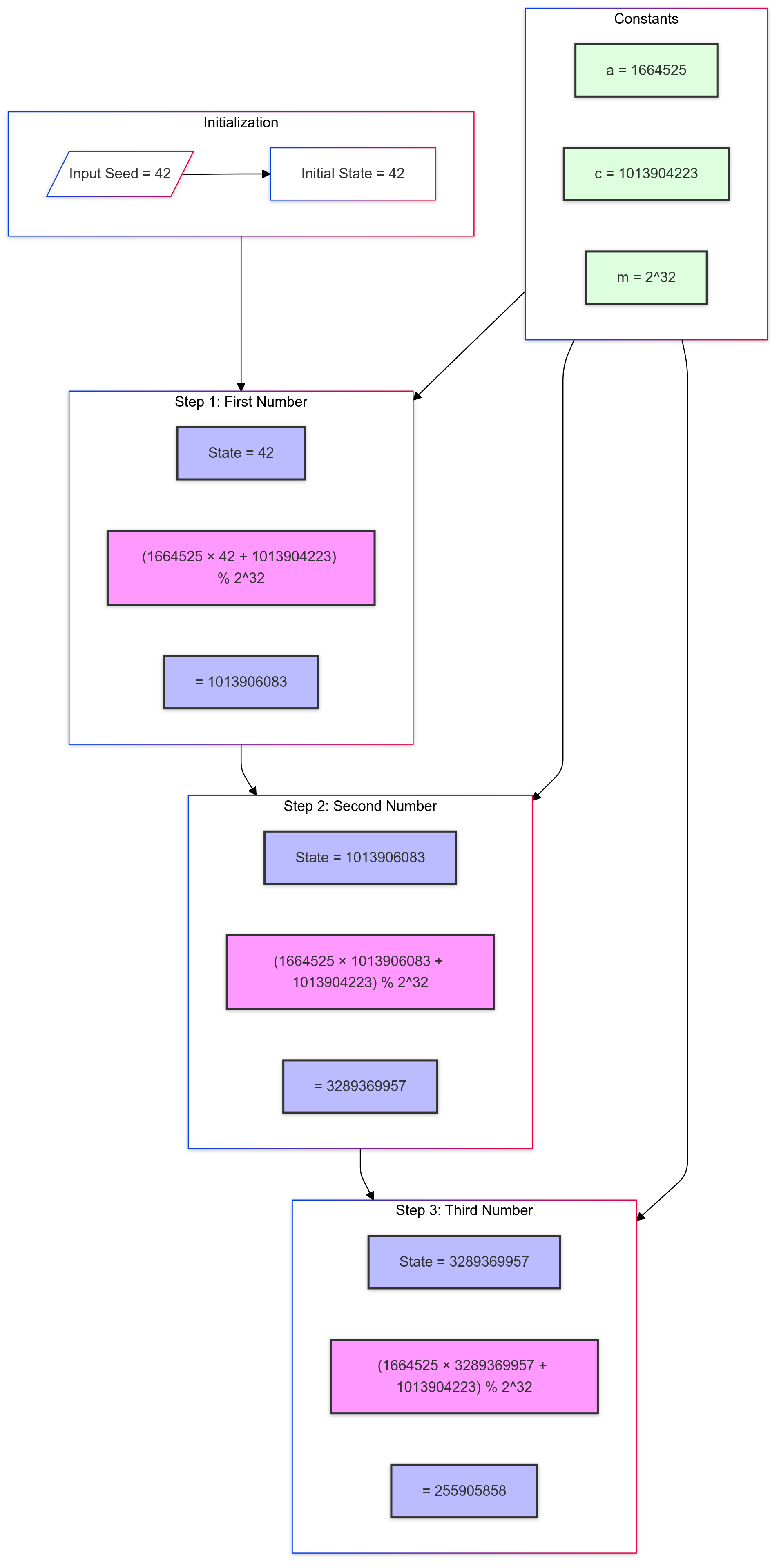
A Pseudorandom Number Generator (PRNG) is basically an algorithm that takes an initial value, called a seed, and produces a sequence of numbers that mimic true randomness. Let's check out a simple example called the Linear Congruential Generator (LCG):
This simple generator shows the core concepts of PRNGs:
- A seed value that kicks off the sequence.
- An internal state that gets updated every time a new number is generated.
- A mathematical formula that transforms the state into something that looks random
It's like a mathematical smoothie blender - throw in a starting number, mix it with some carefully chosen ingredients, and out comes something that looks random!
The Mersenne Twister: Python's Choice
Now, Python doesn't use our simple recipe above. Instead, it uses something way more sophisticated called the Mersenne Twister. It's like upgrading from a hand blender to a professional kitchen mixer. Here's a simplified version of how it works:
Here's a breakdown of what each part does:
- Initialization (
__init__method):- The state array
MThas 624 elements, initially set to zero. - The array is seeded with the initial value (
seed), and the rest of the array is filled using a recurrence relation. - This recurrence ensures that the state evolves in a deterministic but seemingly random way.
- The state array
- Extracting a Random Number (
extract_numbermethod):- This method retrieves a random number from the current state (
MT). - If all 624 numbers have been used (
index >= 624), the state is updated by callingtwist(). - The retrieved number (
y) is then "tempered" — it undergoes a series of bit manipulations to further scramble the value, which helps improve statistical properties and reduce bias.
- This method retrieves a random number from the current state (
- Twisting the State (
twistmethod):- The
twist()function regenerates the state arrayMTby combining elements in a non-linear way. - Specifically, it uses two neighboring values in the state array to create a new one. This step ensures that the sequence retains the required properties of randomness.
- The "twisting" process also involves XOR operations with constants to enhance the randomness.
- The
Mersenne Twister Random Number Generator Visualization
Current seed: 42
Current index: 0 / 624
The Mersenne Twister is popular because it produces a very long sequence of high-quality pseudorandom numbers with a period of %2^{19937}-1%, making it suitable for most applications where randomness is needed, such as simulations or games. However, it is not suitable for cryptographic purposes because its output can be predicted if the internal state is known.
Making Random Numbers Useful
Getting random numbers is just the start. What we really want is to do cool stuff with them. Let's look at some recipes for that:
Uniform Distribution (Random Float)
Explanation:
random_float: Takes the raw 32-bit integer from Mersenne Twister and converts it to a decimal between 0 and 1 by dividing by the maximum possible value %2^{32} - 1%uniform: Scales and shifts that 0-1 number to fit between any two numbersaandb. For example, if you want a number between -1 and 1, it scales 0-1 to span that range
Random Choice (Weighted Sampling)
Explanation:
- Without weights: Simply picks a random index by using modulo (%) to get a number in range
- With weights: Imagine a line divided into segments based on the weights. Generate a random point on that line - whatever segment it falls into is your pick. Bigger weights = bigger segments = more likely to be chosen
Real-World Applications
Monte Carlo Simulations
Monte Carlo methods rely heavily on randomness to estimate numerical results. Here's a classic example that estimates %\pi%:
This elegant approach uses random points to approximate %\pi% through geometric probability. This estimates %\pi% by randomly throwing "darts" at a square with an inscribed circle. If we throw enough darts, the ratio of darts landing inside the circle to total throws approaches %\frac{\pi}{4}%. We multiply by %4% to get %\pi%. This works because:
- The square has area %2 \times 2 = 4%
- The circle has area %\pi% (radius=1)
- %\text{Ratio} = \frac{\pi}{4} = \frac{\text{points inside}}{\text{total points}}%
Machine Learning: Token Sampling for Language Models
In natural language processing (particularly LLM), randomness is often used for token sampling:
Explanation: This selects the next word in AI text generation. The process is:
- Temperature controls randomness (lower = more predictable, higher = more creative)
- Logits (raw scores) are converted to probabilities using softmax
- Words are randomly chosen based on their probabilities
- Higher probability words are more likely to be picked, but not guaranteed
And many more other examples...
True Randomness: When PRNGs Aren't Enough
Sometimes, especially for security stuff, our fake randomness just won't cut it. Instead, modern computers can use hardware events as sources of entropy:
Common sources of hardware entropy include:
- Timing of keystrokes and mouse movements
- Network packet arrival times
- Hardware temperature fluctuations
- Atmospheric noise
- Even tiny quantum effects in the computer's chips!
Tips for Using Random Numbers
Seeding for Reproducibility
Keep Things Separate
Using Built-in Tools
Conclusion
While computers can't generate truly random numbers on their own, the algorithms and techniques we've explored allow us to generate high-quality pseudorandom numbers suitable for most applications. Understanding how these systems work helps us use them effectively and know when we need to reach for true random number sources.
So, the next time you use random.random(), remember: you're not just getting a random number — you're getting the next number in a cleverly crafted sequence designed to look random while being completely deterministic!