ML101.08: Clustering

Trong bài viết này, chúng ta sẽ tìm hiểu về khái niệm clustering. Đây là một lớp các thuật toán phân cụm trong học máy. Phân cụm hay gom cụm, phân nhóm được dùng rất nhiều trong quá trình phân tích và tìm hiểu về dữ liệu. Phân cụm giúp chúng ta hiểu được phần nào mối tương quan giữa các điểm dữ liệu với nhau, và một ứng dụng quan trọng của nó chính là phát hiện ngoại lai (outlier detection). Ngoài ra, chúng ta hoàn toàn có thể ứng dụng phương pháp phân cụm cho bài toán phân loại.

Giả sử ta xét một bài toán phân loại nhưng không có bất kỳ nhãn nào như sau:

Cho các điểm dữ liệu %x_1, x_2,..,x_N%. Hãy phân các điểm này thành %K% loại với số %K% cho trước.

Có thể thấy bài toán này khác với các bài toán thông thường vì chúng ta chỉ có dữ liệu %x% chứ không có nhãn %y%. Do đó bài toán này được gọi là bài toán học không giám sát (unsupervised learning). Để giải quyết bài toán này, ta sử dụng một ý tưởng đơn giản đó là nếu hai điểm dữ liệu thuộc cùng một lớp thì khoảng cách giữa chúng sẽ gần nhau hơn là so với hai điểm dữ liệu không cùng lớp. Bình thường khi có %x% và %y%, chúng ta chỉ cần quan tâm về việc gán đúng nhãn %y_i% cho %x_i% mà thôi. Tuy nhiên do bài toán này không có nhãn nên ta chỉ có thể khai thác mối quan hệ giữa các điểm dữ liệu %x% với nhau. Lưu ý, khoảng cách mà chúng ta nói đến ở đây chính là khoảng cách trong không gian vector.

K-Means

Xuất phát từ ý tưởng đó, ta có một thuật toán rất nổi tiếng có tên K-Means clustering. Trong thuật toán này, ta cần quan tâm một số khái niệm như sau:

• %K%: Đây là số lượng cụm mà chúng ta muốn phân chia, đây là đầu vào cho trước của một thuật toán K-Means bất kỳ.
• Centroid hay tâm chính là điểm đại diện của một cụm. Ví dụ ta có một cụm gồm 3 điểm dữ liệu %(x_1, x_2, x_3)% thì ta có thể lấy điểm ở giữa của các cụm này làm centroid: %x_\text{centroid} = \frac{x_1 + x_2 + x_3}{3}%. Vì thế, với %K% cụm ta sẽ có %K% centroid.

Thuật toán phân cụm K-Means gồm các bước sau:

• Bước 1: Khởi tạo %K% centroid ban đầu bằng cách chọn ra %K% điểm bất kỳ trong tập dữ liệu.
• Bước 2: Phân các điểm dữ liệu còn lại vào các cụm với nguyên tắc điểm dữ liệu đó gần với centroid nào nhất thì thuộc cụm của centroid đó.
• Bước 3: Tính toán lại centroid của cụm sau khi đã có thêm một số điểm dữ liệu mới được cho vào cụm với công thức: $$x_\text{centroid}^i = \frac{1}{N}\sum_{j \in \text{cluster}_i}{x_j}$$
• Bước 4: Lặp lại bước 2 và bước 3 cho đến khi đạt được điều kiện dừng hoặc các centroid không thay đổi nữa.

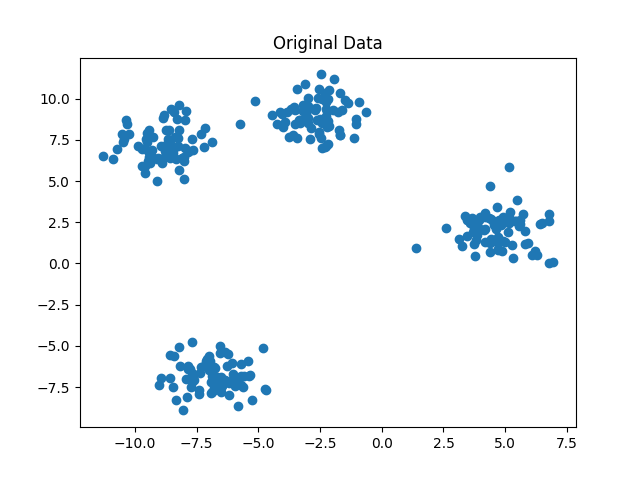
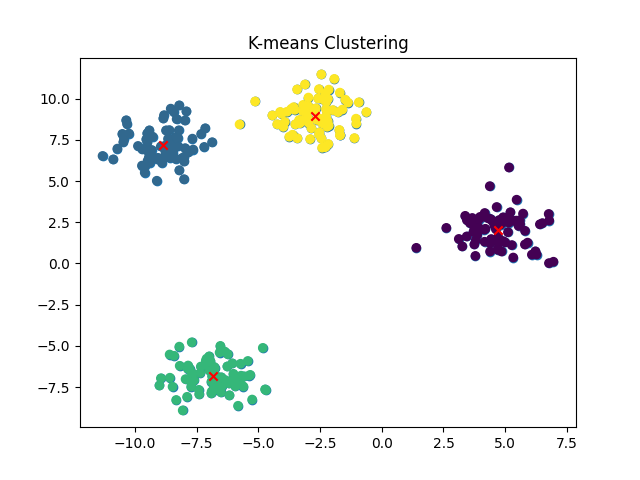
Trong quá trình lặp, các điểm dữ liệu sẽ được phân vào các cụm tương ứng với centroid gần nhất. Sau đó, vị trí của centroid sẽ được cập nhật bằng cách tính trung bình của tất cả các điểm dữ liệu trong cùng một cụm. Quá trình này sẽ được lặp lại cho đến khi không có sự thay đổi nào trong việc phân chia dữ liệu hoặc đạt được điều kiện dừng được thiết lập trước đó, điều kiện đó có thể là giới hạn số lần lặp của thuật toán.

Kết quả của thuật toán K-means clustering là một tập hợp các cụm, mỗi cụm chứa các điểm dữ liệu có đặc trưng tương tự nhau và khác với các điểm dữ liệu trong những cụm khác. Các cụm này có thể được sử dụng để phân tích và trực quan hóa dữ liệu, giúp chúng ta hiểu được các mối quan hệ và xu hướng trong dữ liệu của mình.

K-means clustering là một thuật toán phân cụm dữ liệu đơn giản và hiệu quả. Tuy nhiên, như mọi thuật toán khác, nó cũng có những điểm mạnh và điểm yếu như sau:

Điểm mạnh:

• K-means là một thuật toán nhanh và hiệu quả, đặc biệt là với những tập dữ liệu lớn.
• K-means có thể được áp dụng cho nhiều loại dữ liệu khác nhau và có thể được sử dụng trong nhiều lĩnh vực khác nhau, chẳng hạn như thị trường tài chính, y học, kinh doanh, và khoa học dữ liệu.
• K-means cho phép phân loại dữ liệu thành các nhóm dựa trên các đặc trưng của chúng, giúp chúng ta hiểu được các mối quan hệ và xu hướng trong dữ liệu của mình.
• K-means có thể được sử dụng để giảm số chiều của dữ liệu và giúp chúng ta hiểu được dữ liệu một cách trực quan hơn.

Điểm yếu:

• Một trong những điểm yếu của K-means là phải xác định trước số lượng nhóm cần phân loại. Việc chọn số lượng nhóm phù hợp có thể khó khăn đối với những người mới bắt đầu.
• K-means có thể dẫn đến kết quả không tối ưu và phụ thuộc rất nhiều vào vị trí ban đầu của các centroid.
• K-means chỉ hoạt động tốt đối với các cấu trúc dữ liệu tròn và đồng nhất, nhưng không phù hợp với các cấu trúc dữ liệu phức tạp, không đồng nhất hoặc có nhiễu.
• K-means có thể bị ảnh hưởng bởi các điểm dữ liệu ngoại lai (outlier) và có thể cho kết quả không chính xác nếu không xử lý outlier đúng cách.

Độ phức tạp tính toán của thuật toán K-means có thể được phân tích dựa trên ba yếu tố chính: số lượng điểm dữ liệu (%N%), số lượng cụm (%K%) và số lượng vòng lặp (%I%). Độ phức tạp của thuật toán K-means được xác định bởi tổng số phép tính cần thực hiện trong quá trình phân cụm.

Trong mỗi vòng lặp, thuật toán K-means thực hiện hai bước chính: gán điểm dữ liệu vào cụm gần nhất và cập nhật tâm (centroid) của mỗi cụm.

1. Gán điểm dữ liệu vào cụm gần nhất: Đối với mỗi điểm dữ liệu, thuật toán cần tính khoảng cách đến tất cả các centroid và chọn ra centroid gần nhất. Do đó, số lượng phép tính trong bước này là %N \times K%.
2. Cập nhật tâm của mỗi cụm: Sau khi gán các điểm dữ liệu vào cụm, thuật toán cần tính toán lại tâm của mỗi cụm bằng cách tính trung bình cộng của tất cả các điểm dữ liệu trong cụm đó. Số lượng phép tính cần thiết trong bước này là %N \times K%.

Như vậy, trong mỗi vòng lặp, số lượng phép tính cần thực hiện là% (N \times K) + (N \times K) = 2 \times N \times K%.

Nếu thuật toán K-means chạy trong %I% vòng lặp, tổng số phép tính cần thực hiện sẽ là %2\times N \times K \times I%. Do đó, độ phức tạp tính toán của thuật toán K-means là %O(N \times K \times I)%.

Trong thực tế, số lượng vòng lặp I thường không quá lớn, và thuật toán K-means hội tụ khá nhanh. Tuy nhiên, độ phức tạp tính toán của K-means vẫn có thể trở nên đáng kể nếu số lượng điểm dữ liệu N hoặc số lượng cụm K lớn. Để giảm bớt độ phức tạp này, có thể sử dụng các biến thể của thuật toán K-means như K-means++ (cải tiến khởi tạo centroid) hoặc Mini-Batch K-means (sử dụng một tập con của dữ liệu trong mỗi vòng lặp) để tăng tốc độ hội tụ và giảm thời gian tính toán.

DBSCAN

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) là một thuật toán phân cụm dựa trên mật độ, cho phép xác định cụm có hình dạng tùy ý và phát hiện ngoại lai (outliers) hiệu quả. Thuật toán này không yêu cầu xác định số lượng cụm trước khi thực hiện phân cụm, điều này giúp DBSCAN khác biệt so với thuật toán K-means.

Thuật toán DBSCAN xem xét hai tham số chính:

• Epsilon (ε): Khoảng cách lân cận mà thuật toán sẽ xem xét để xác định các điểm dữ liệu liên quan.
• MinPts: Số lượng tối thiểu các điểm dữ liệu trong một cụm để được coi là một cụm hợp lệ.

Các bước thực hiện thuật toán DBSCAN như sau:

• Xác định các điểm lân cận của mỗi điểm dữ liệu trong tập dữ liệu dựa trên giá trị Epsilon (ε).
• Gán nhãn cho các điểm dữ liệu dựa trên MinPts: (1) Nếu một điểm có số lượng điểm lân cận >= MinPts, gán nhãn cho điểm đó là một điểm chủ đạo (core point). (2) Nếu một điểm không phải là điểm chủ đạo nhưng có ít nhất một điểm chủ đạo trong lân cận, gán nhãn cho điểm đó là một điểm biên (border point). (3) Nếu một điểm không thuộc vào hai loại trên, gán nhãn cho điểm đó là một ngoại lai (noise point).
• Hợp nhất các điểm chủ đạo liên quan để tạo thành các cụm, sau đó gán các điểm biên vào cụm tương ứng của chúng.

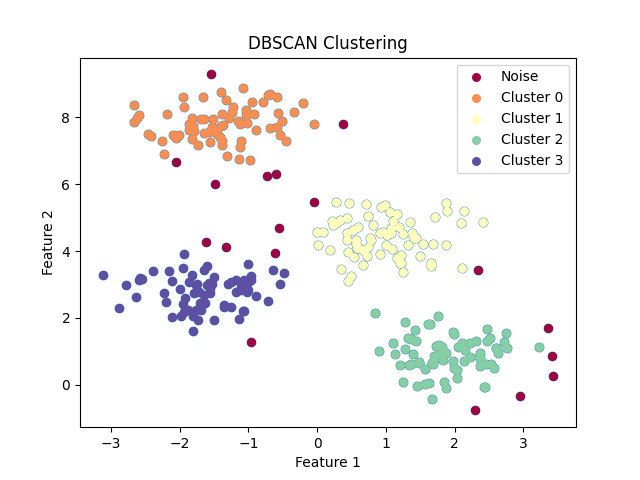
Độ phức tạp của thuật toán DBSCAN phụ thuộc vào cấu trúc dữ liệu và cách lưu trữ dữ liệu. Nếu dữ liệu được lưu trữ hiệu quả trong một cấu trúc cây, độ phức tạp của DBSCAN sẽ là %O(N \times \log{N})%, trong đó %N% là số lượng điểm dữ liệu. Tuy nhiên, nếu dữ liệu không được lưu trữ hiệu quả, độ phức tạp có thể lên đến %O(N^2)% do việc tính toán khoảng cách giữa các điểm dữ liệu. Mặc dù độ phức tạp của DBSCAN có thể cao hơn K-means, nhưng thuật toán này lại cho phép phát hiện các cụm có hình dạng phức tạp hơn và xác định ngoại lai một cách hiệu quả. Điều này làm cho DBSCAN trở thành một lựa chọn phù hợp cho những tình huống mà dữ liệu có cấu trúc phức tạp và số lượng cụm không xác định trước.

Spectral Clustering

Spectral Clustering là một thuật toán phân cụm dựa trên đồ thị, được sử dụng để phân chia dữ liệu thành các cụm mà không yêu cầu giả định về hình dạng của chúng. Spectral Clustering sử dụng thông tin về đồ thị để tạo ra các cụm có độ liên kết cao bên trong và độ liên kết thấp giữa các cụm.

Các bước của thuật toán Spectral Clustering:

• Tính ma trận tương tự giữa các điểm dữ liệu.
• Xây dựng đồ thị từ ma trận tương tự (thường là dạng đồ thị k-lân cận hoặc đồ thị epsilon).
• Tính toán ma trận Laplacian từ đồ thị.
• Tính các vector riêng của ma trận Laplacian và chọn k vector riêng nhỏ nhất tương ứng với k cụm mong muốn.
• Xây dựng ma trận mới từ các vector riêng và chuẩn hóa các hàng.
• Áp dụng thuật toán phân cụm như K-means trên ma trận mới để tạo ra các cụm cuối cùng.

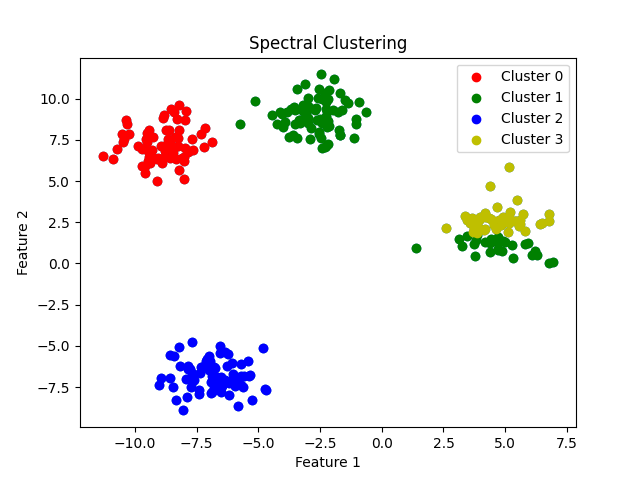
Độ phức tạp thời gian của thuật toán Spectral Clustering phụ thuộc vào các bước tính toán ma trận tương tự, ma trận Laplacian và giải bài toán vector riêng. Độ phức tạp thời gian của thuật toán là O(N^3), trong đó N là số lượng điểm dữ liệu. Tuy nhiên, trong thực tế, độ phức tạp thời gian thường thấp hơn nhiều so với lý thuyết, nhờ vào các kỹ thuật tối ưu hóa và tính toán gần đúng trong việc giải quyết bài toán vector riêng.

Mặc dù Spectral Clustering có độ phức tạp thời gian cao hơn so với K-means, nó lại có ưu điểm trong việc xử lý các cụm dữ liệu có hình dạng phức tạp, không đồng nhất hoặc các cụm dữ liệu không tách biệt theo các đặc trưng không gian. Bằng cách sử dụng thông tin đồ thị để tìm ra cấu trúc của dữ liệu, Spectral Clustering không bị hạn chế bởi các giả định về hình dạng và phân bố của dữ liệu như K-means.

Một số ưu điểm của thuật toán Spectral Clustering:

• Khả năng phân cụm dữ liệu có cấu trúc phức tạp và không đồng nhất.
• Không yêu cầu giả định về hình dạng và phân bố của dữ liệu.
• Tận dụng thông tin đồ thị để tìm ra cấu trúc của dữ liệu.

Một số nhược điểm của thuật toán Spectral Clustering:

• Độ phức tạp thời gian cao, đặc biệt là với các tập dữ liệu lớn.
• Cần xác định trước số lượng cụm.
• Có thể bị ảnh hưởng bởi các điểm dữ liệu ngoại lai nếu không xử lý chúng đúng cách.

Trong một số trường hợp, Spectral Clustering có thể mang lại kết quả tốt hơn so với các thuật toán phân cụm khác như K-means và DBSCAN. Tuy nhiên, việc lựa chọn thuật toán phù hợp sẽ phụ thuộc vào yêu cầu của bài toán, đặc trưng của dữ liệu và nguồn lực tính toán có sẵn.

Hierarchical Clustering

Hierarchical Clustering (Phân cụm phân cấp) là một kỹ thuật phân cụm dữ liệu dựa trên cấu trúc cây phân cấp (hierarchical tree). Có hai phương pháp chính trong Hierarchical Clustering là Agglomerative (phân cụm động tụ) và Divisive (phân cụm phân tách). Trong bài viết này, chúng ta sẽ tập trung vào phương pháp Agglomerative.

Agglomerative Hierarchical Clustering bắt đầu bằng việc xem mỗi điểm dữ liệu là một cụm riêng lẻ, sau đó lặp lại quá trình sau: tìm hai cụm gần nhất và hợp nhất chúng lại thành một cụm mới. Quá trình này được lặp lại cho đến khi chỉ còn một cụm duy nhất chứa tất cả các điểm dữ liệu.

Các bước thực hiện của Agglomerative Hierarchical Clustering:

• Khởi tạo: Mỗi điểm dữ liệu là một cụm riêng lẻ.
• Tính toán ma trận khoảng cách giữa các cụm.
• Tìm hai cụm có khoảng cách nhỏ nhất, hợp nhất chúng thành một cụm mới.
• Cập nhật ma trận khoảng cách.
• Lặp lại bước 3 và 4 cho đến khi chỉ còn một cụm duy nhất chứa tất cả các điểm dữ liệu.

Ma trận khoảng cách giữa các cụm có thể được tính toán dựa trên các tiêu chí khác nhau như Single Linkage (khoảng cách giữa hai điểm gần nhất trong hai cụm), Complete Linkage (khoảng cách giữa hai điểm xa nhất trong hai cụm) hoặc Average Linkage (trung bình khoảng cách giữa tất cả các cặp điểm trong hai cụm).

Độ phức tạp thời gian của Agglomerative Hierarchical Clustering là %O(N^3)%, trong đó n là số lượng điểm dữ liệu. Độ phức tạp này chủ yếu phát sinh từ việc cập nhật ma trận khoảng cách sau mỗi lần hợp nhất hai cụm. Trong trường hợp dữ liệu lớn, độ phức tạp này có thể trở thành một hạn chế đáng kể.

Tuy nhiên, có các cải tiến về thuật toán để giảm độ phức tạp thời gian xuống %O(N^2 \log{N})% hoặc thậm chí %O(N^2)% sử dụng cấu trúc dữ liệu hiệu quả hơn như Priority Queue (hàng đợi ưu tiên) hoặc các thuật toán tìm cây bao trùm nhỏ nhất.

Hierarchical Clustering là một kỹ thuật phân cụm mạnh mẽ, đặc biệt hữu ích khi chúng ta không biết trước số lượng cụm mong muốn. Tuy nhiên, độ phức tạp tính toán của nó có thể làm giảm hiệu quả khi áp dụng trên tập dữ liệu lớn.

Kết

Trong bài viết này, chúng ta đã tìm hiểu về các thuật toán phân cụm phổ biến trong học máy, bao gồm K-means, DBSCAN, Spectral Clustering và Hierarchical Clustering. Mỗi thuật toán có những đặc điểm, ưu điểm và nhược điểm riêng, do đó việc lựa chọn phù hợp sẽ phụ thuộc vào bài toán cụ thể và tính chất của dữ liệu.

K-means là một thuật toán đơn giản và hiệu quả, thích hợp cho dữ liệu lớn và có cấu trúc đơn giản. DBSCAN cung cấp khả năng xử lý dữ liệu có nhiễu và cấu trúc phức tạp, cũng như tự động xác định số lượng cụm. Spectral Clustering cho phép phân cụm dữ liệu theo các đặc trưng không gian, phù hợp với dữ liệu có cấu trúc phức tạp và không tuyến tính. Hierarchical Clustering cung cấp một cách tiếp cận linh hoạt để tìm số lượng cụm tối ưu, nhưng độ phức tạp tính toán cao hơn so với các phương pháp khác.

Khi sử dụng các thuật toán phân cụm, nên thực nghiệm với nhiều phương pháp khác nhau để tìm ra phương pháp phù hợp nhất cho bài toán của bạn. Đồng thời, việc tiền xử lý dữ liệu, xử lý ngoại lệ và chọn độ đo khoảng cách phù hợp cũng rất quan trọng để đạt được kết quả phân cụm tốt.