How to Control the Creativity of LLMs Using the Temperature Parameter

When working with Large Language Models (LLMs), one of the most powerful yet often misunderstood parameters is "temperature". This setting acts as a creativity dial, allowing you to fine-tune the model's output between deterministic precision and creative exploration. Let's dive into what temperature means and how to use it effectively.

What is Temperature?

Temperature is a parameter that controls the randomness in the model's token selection process. It's expressed as a positive real number %(\text{T} > 0)% that affects the model's behavior in different ways:

• Very low temperature (%\text{T} \rightarrow 0%, approaching but never exactly 0): The model becomes nearly deterministic, consistently selecting the highest probability tokens. This makes it ideal for tasks requiring high precision.
• Neutral (%\text{T} = 1%): The model maintains the original probability distribution of tokens without scaling, serving as a balanced setting for general text generation.
• High temperature (%\text{T} > 1%): The model flattens the probability distribution, increasing the likelihood of selecting lower-probability tokens, which leads to more diverse and creative outputs (typically used up to 2.0)

The Mathematics Behind

Temperature scaling fundamentally alters the probability distribution used for selecting the next token in the sequence. Here's how it works, demonstrated with Python code:

In this example, the temperature %\text{T}% affects the probability distribution by adjusting the logits:

1. Scaling logits: %\mathbf{l} = [l_1, ..., l_n]%, temperature scaling gives: %l'_i = \frac{l_i}{\text{T}}%
2. Softmax transformation: The probability of selecting token %i% becomes: $$p(x_i)= \frac{\exp(l'_i)}{\sum_j \exp(l'_j)}$$
3. Effect on probability ratios: For tokens %i% and %j%, %\frac{p(x_i)}{p(x_j)} = \exp(\frac{l_i - l_j}{\text{T}})%:
   • As %\text{T} \to 0%, this ratio approaches %\infty% if %l_i > l_j%, creating a deterministic selection,
   • As %\text{T} \to \infty%, the ratio approaches 1, creating a uniform distribution.
   • At %\text{T} = 1%, we maintain the original logit differences.

Visualization of Temperature Effects

Here’s how different temperatures affect probability distributions:

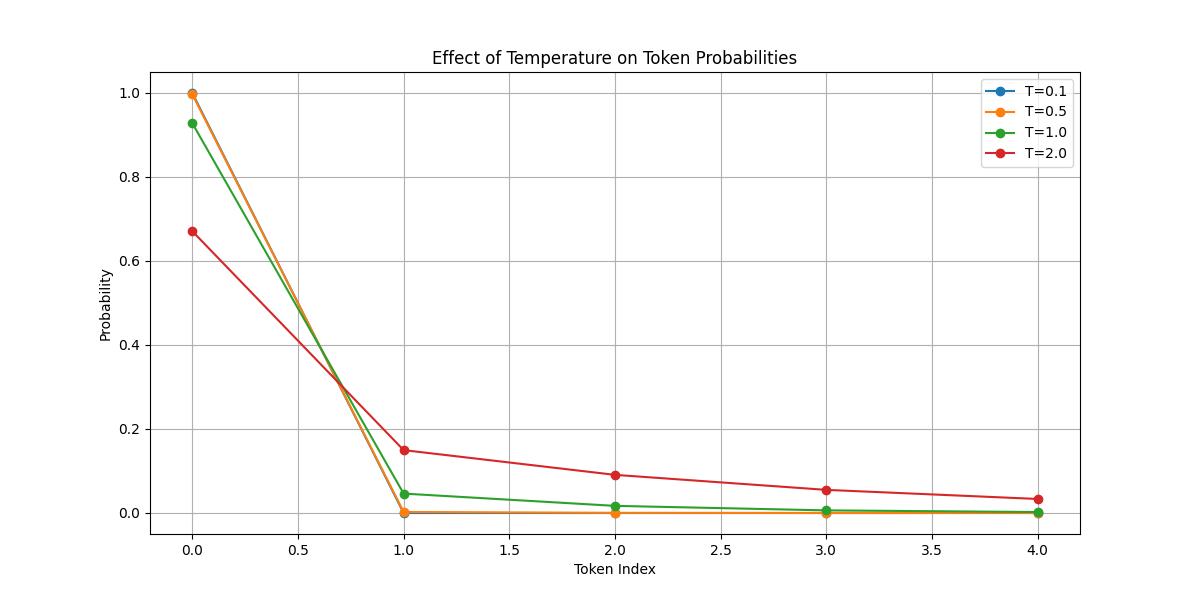
You can also try the interactive visualization below:

As you can see, a higher temperature gives us a greater chance of selecting tokens other than cat. When the temperature approaches 0, the results become more deterministic.

Real World Example

Here’s a practical example from Llama's codebase on GitHub, which applies temperature-based scaling:

In this implementation, after adjusting probabilities with temperature, efficient sampling is key. The Llama-3 model's implementation of top-p (nucleus) sampling sorts probabilities in descending order, tracks original indices, and computes cumulative sums. When cumulative probability exceeds threshold p, remaining probabilities are zeroed out. The function then renormalizes and samples from this filtered distribution using multinomial sampling, mapping the sample back to the original token. For example, with %p=0.9% and probabilities %[0.5, 0.3, 0.1, 0.1]%, it keeps only the first three tokens %([0.5, 0.3, 0.1])% and samples from the renormalized distribution %[0.56, 0.33, 0.11]%.

In practice, many commercial LLM APIs like OpenAI's GPT series scale the temperature parameter to a more user-friendly range of 0 to 1, rather than the theoretical range of 0 to infinity. This normalization makes the parameter more intuitive to work with while maintaining the same fundamental effects:

• OpenAI GPT-4/3.5: Temperature range [0, 1] where 0.7 is considered neutral
• Claude: Temperature range [0, 1] with 0.7 as default
• PaLM: Temperature range [0, 1] with 0.7 as default

This scaling is typically done internally, where the API's temperature value is multiplied by a scaling factor before being applied to the logits. For example, a temperature of 0.8 in the API might be scaled to 1.6 internally.

Conclusions

In this post, we explored how temperature affects LLM outputs by adjusting the token probability distribution. When selecting a temperature value for your LLM application, consider these key guidelines:

• For factual/analytical tasks (T ≈ 0.1–0.3):
  • Mathematical calculations, fact-based Q&A, code completion.
• For balanced tasks (T ≈ 0.4–0.7):
  • General conversation, business writing, translation, summarization.
• For creative tasks (T ≈ 0.8–1.0):
  • Creative writing, brainstorming, poetry, exploratory dialogue.

If you find my post useful, please consider subscribing to my blog to receive more articles and tips in the future.