ML101.06: Gaussian Discriminant Analysis

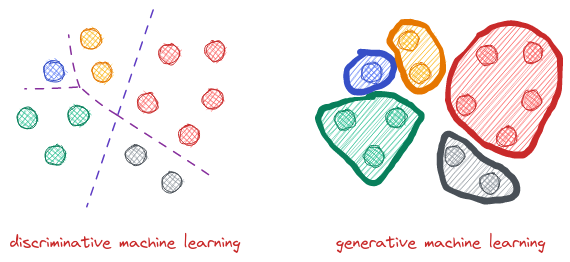
Chúng ta đã tìm hiểu về một số thuật toán như Linear Regression, Logistic Regression, Softmax Regression,.. Tất cả các thuật toán này điều có điểm chung đó là chúng ta đều đi phân bố xác suất %p(y\mid x; \theta%), tức là tìm phân bố xác suất có điều kiện của %y% theo biến ngẫu nhiên %x%. Do đó, nhóm thuật toán này được gọi là các thuật toán Discriminative Machine Learning. Ngoài Discriminative Machine Learning, chúng ta còn một nhóm các thuật toán lớn nữa đó là Generative Machine Learning. Đây có thể xem là hai góc nhìn, hai hướng tiếp cận của một bài toán. Nếu như DML mô hình bài toán thành tìm trực tiếp phân bố xác suất %p(y \mid x; \theta)% thì GML lại đi tìm phân bố %p(y \mid x; \theta)% thông qua phân bố %p(x\mid y; \theta)%.
Ví dụ ta xét bài toán đó là phân loại hình ảnh giữa chó và mèo. Các hình ảnh này được biến đổi thành vector chứa các đặc trưng của hình ảnh %x \in \mathbb{R}^k%. Những thuật toán như Logistic Regression hoặc Softmax Regression sẽ tìm một đường phân cách (decision boundary) để chia không gian đặc trưng %\mathbb{R}^k% thành hai nữa. Một nữa thuộc về các điểm dữ liệu có nhãn là chó và một nữa dành cho dữ liệu có nhãn là mèo. Từ đó, ta có thể quyết định xem một hình ảnh chưa nhìn thấy bao giờ (unseen data) thuộc loại nào bằng cách kiểm tra xem vector đặc trưng của hình ảnh đó thuộc về phía bên nào của decision boundary.
Tuy nhiên, Generative Machine Learning sẽ có một cách tiếp cận khác. Đó là thay vì tìm trực tiếp decision boundary, các thuật toán GML đầu tiên sẽ đi tìm mô hình của từng loại dữ liệu. Chúng ta phải tìm hai mô hình cho hai lớp là chó và mèo. Sau đó để phân loại, chúng ta chỉ cần thực hiện so khớp (matching) dữ liệu mới với mô hình đã có xem dữ liệu đó trùng khớp mô hình chó hơn hay mô hình mèo hơn. Một cách đơn giản hơn thì ta có thể hiểu rằng Discriminative Machine Learning đi tìm sự khác biệt giữa chó và mèo. Còn Generative Machine Learning thì đi tìm xem hình ảnh của một con mèo và một con chó trong như thế nào và so khớp với dữ liệu mới.

Ở trên là ví dụ về bài toán phân loại chỉ với hai lớp. Đối với bài toán nhiều lớp hơn thì ý tưởng cũng tương tự như vậy. Chỉ khác là boundary decision của DML sẽ có dạng hình phức tạp hơn mà thôi.
Diễn giải bằng ngôn ngữ xác suất thì đối với Generative Machine Learning, thay vì đi tìm %p(y\mid x)%, chúng ta đi tìm %p(x\mid y)% và %p(y)%. Nếu kí hiệu lớp "chó" là %0% và lớp "mèo" là %1% thì ta có %p(x\mid y=0)% là mô hình vector đặc trưng của chó, còn %p(x\mid y=1)% là mô hình vector đặc trưng của mèo. Trong khi đó %p(y)% được gọi là phân phối tiên nghiệm (prior distribution). Do %p(y)% thông thường chính là phân phối nhãn của dữ liệu và có thể tính trực tiếp hoặc dựa vào kinh nghiệm để đưa ra cho nên chúng ta không cần phải "học" phân bố này. Ví dụ, một tập dữ liệu gồm 10 mẫu, trong đó có 4 mẫu có nhãn là "chó", 6 mẫu có nhãn là "mèo" thì ta có %p(y=0)=0.4% và %p(y=1)=0.6%. Cái chúng ta cần học đó chính là %p(x\mid y)%. Sau khi đã có hai thông tin %p(x\mid y)% và %p(y)% thì kết quả của bài toán - tức phân phối hậu nghiệm (posterior distribution) %p(y\mid x)% có thể được tính bằng công thức Bayes như sau:
$$p(y \mid x)=\frac{p(x \mid y) p(y)}{p(x)}\tag{1}$$
Trong công thức trên, do mẫu số %p(x)=p(x\mid y=0)p(y=0) + p(x\mid y=1)p(y=1)%. Nên thực tế chúng ta chỉ cần tìm %p(x\mid y)%, đây cũng chính là mục tiêu quan trọng nhất của Generative Machine Learning.
Gaussian Discriminant Analysis
Gaussian Discriminant Analysis (GDA) là một trong những mô hình cơ bản nhất của Generative Machine Learning. Mô hình này được gọi là Gaussian Discriminant Analysis bởi vì trong mô hình này chúng ta phải giả định %p(x\mid y)% là một phân bố chuẩn cho dữ liệu nhiều chiều (multivariate normal distribution).
Đầu tiên, chúng ta cần có một chút khái niệm về phân bố chuẩn nhiều chiều. Đây là khái niệm tổng quát hơn của phân bố chuẩn đơn biến (một chiều dữ liệu). Phân bố chuẩn nhiều chiều của biến ngẫu nhiên %X \in \mathbb{R}^d% có dạng:
$$X \sim \mathcal{N}(\mu, \Sigma)\tag{2}$$
Trong đó,
- %\mu \in \mathbb{R}^d% là vector trung bình, %\mu = \mathrm{E}[X]=\int_x x p(x ; \mu, \Sigma) d x%.
- %\Sigma \in \mathbb{R}^{d\times d}% là ma trận hiệp phương sai, %\Sigma=\text{Cov}(X)=\mathrm{E}\left[Z Z^T\right]-(\mathrm{E}[Z])(\mathrm{E}[Z])^T%.
Hàm mật độ xác suất của %(2)% có dạng như sau:
$$p(x ; \mu, \Sigma)=\frac{1}{(2 \pi)^{d / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu)\right)\tag{3}$$
Trở lại với bài toán phân lớp nhị phân, nếu sử dụng phân bố chuẩn nhiều chiều để mô hình hóa %p(x\mid y)% thì ta sẽ có mô hình như sau:
$$\begin{aligned}y & \sim \operatorname{Bernoulli}(\phi) \\x \mid y=0 & \sim \mathcal{N}\left(\mu_0, \Sigma\right) \\x \mid y=1 & \sim \mathcal{N}\left(\mu_1, \Sigma\right)\end{aligned}\tag{4}$$
Từ đó suy ra các hàm mật độ xác xuất bên dưới:
$$\begin{aligned}p(y) &=\phi^y(1-\phi)^{1-y} \\p(x \mid y=0) &=\frac{1}{(2 \pi)^{d / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}\left(x-\mu_0\right)^T \Sigma^{-1}\left(x-\mu_0\right)\right) \\p(x \mid y=1) &=\frac{1}{(2 \pi)^{d / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}\left(x-\mu_1\right)^T \Sigma^{-1}\left(x-\mu_1\right)\right)\end{aligned}\tag{5}$$
Có thể thấy các tham số của mô hình bao gồm %\phi, \mu_1, \mu_2, \Sigma%. Tương tự như các phương pháp khác, chúng ta tiếp tục đi maximize log-likelihood của %p(x\mid y)% trên tập dữ liệu %D=\{(x_1, y_1), (x_2, y_2),..., (x_n, y_n)\}%:
$$\begin{aligned}\ell\left(\phi, \mu_0, \mu_1, \Sigma\right) &=\log \prod_{i=1}^n p\left(x_{i}, y_{i} ; \phi, \mu_0, \mu_1, \Sigma\right) \\&=\log \prod_{i=1}^n p\left(x_{i} \mid y_{i} ; \mu_0, \mu_1, \Sigma\right) p\left(y_{i} ; \phi\right)\end{aligned}\tag{6}$$
Bằng cách maximize %\ell% theo từng tham số, ta được các công thức như sau:
$$\begin{aligned}\{\phi, \mu_0, \mu_1, \Sigma\}&=\arg \max_{\phi, \mu_0, \mu_1, \Sigma}\ell(\phi, \mu_0, \mu_1, \Sigma)\\\implies \phi &=\frac{1}{n} \sum_{i=1}^n 1\left\{y^{(i)}=1\right\}, \\\mu_0 &=\frac{\sum_{i=1}^n 1\left\{y^{(i)}=0\right\} x^{(i)}}{\sum_{i=1}^n 1\left\{y^{(i)}=0\right\}}, \\\mu_1 &=\frac{\sum_{i=1}^n 1\left\{y^{(i)}=1\right\} x^{(i)}}{\sum_{i=1}^n 1\left\{y^{(i)}=1\right\}}, \\\Sigma &=\frac{1}{n} \sum_{i=1}^n\left(x^{(i)}-\mu_{y^{(i)}}\right)\left(x^{(i)}-\mu_{y^{(i)}}\right)^T.\end{aligned}\tag{7}$$
Có thể hình dung hai phân bố mà GDA đi tìm bằng các hình ảnh như ví dụ dưới đây:

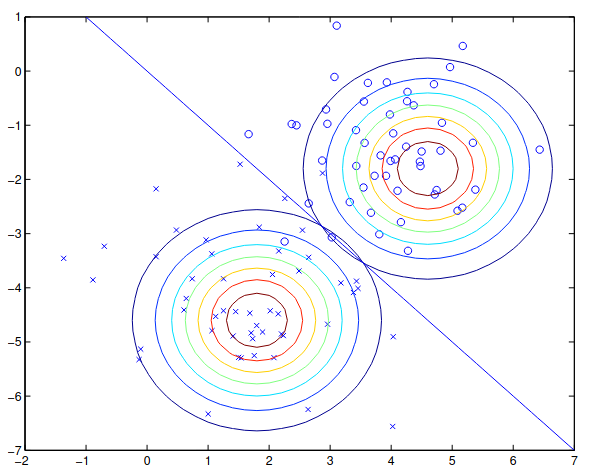

Gaussian Discriminant Analysis vs Logistic Regression
Nếu ta xem %p(y=1\mid x; \phi, \mu_0, \mu_1, \Sigma)% được tham số số bởi một hàm số phụ thuộc %x% thay vì bộ tham số %\phi, \mu_0, \mu_1, \Sigma%. Thì ta có thể viết lại giá trị trên thành %p(y=1\mid x; \theta)%, trong đó %\theta% là một hàm theo biến %x%. Khi đó, ta cũng có thể mô hình hóa giá trị xác suất này bằng hàm sigmoid như sau:
$$p\left(y=1 \mid x ; \phi, \Sigma, \mu_0, \mu_1\right)=\frac{1}{1+\exp \left(-\theta^T x\right)}\tag{8}$$
Đây chính là dạng của mô hình Logistic Regression. Tuy có một mối liên kết gần gũi như vậy, nhưng điểm khác biệt rõ ràng nhất giữa hai mô hình là ở các giả định về mặt dữ liệu. Ta có thể thấy GDA yêu cầu một giả định dữ liệu nghiêm ngặt hơn Logistic Regression rất nhiều đó là dữ liệu phải được mô hình hóa bằng phân bố chuẩn. Do đó, nếu thật sự phân bố xác suất của dữ liệu là phân bố chuẩn thì GDA sẽ hoạt động tốt hơn Logistic Regression. Ngược lại, do không có yêu cầu cụ thể về mặt phân bố của dữ liệu cho nên Logistic Regression sẽ hoạt động tốt hơn với những tập dữ liệu không thật sự được lấy mẫu từ phân bố chuẩn. Từ đó, Logistic Regression cũng xử lý tốt hơn các tình huống dữ liệu được coi là ngoại lai (outliers) đối với GDA. Điều này dẫn đến việc Logistic Regression có tính tổng quát cao hơn và được sử dụng thực tế nhiều hơn so với GDA.
Tuy nhiên, đây chỉ là so sánh về hiệu quả phân lớp của mô hình GDA (đại diện cho generative model) với Logisctic Regression (đại diện cho discriminative model). Chúng ta phải kể đến một ứng dụng rất quan trọng khác hoặc có thể nói là chính yếu của Generative Machine Learning đó là giúp giải quyết các bài toán tạo sinh (generative). Các ứng dụng như AI vẽ tranh, sinh ảnh, tổng hợp tiếng nói, viết văn,.. đều là những thành tựu của các Generative Model. Các mô hình sinh dạng này sẽ là những chủ đề mà chúng ta sẽ tìm hiểu ở các bài viết chuyên sâu hơn.